量子力学 概率统计在量子力学中的应用

 

概率统计在量子力学中的应用很广泛，如几率波，以及20世纪初期，量子力学逐步发展起来时，对于微观粒子中的费密子和玻色子分别建立费米－狄拉克统计和玻色—爱因斯坦统计都是基于概率统计得到的。以下分别介绍几率波、费米—狄拉克统计和玻色爱因斯坦：

一、几率波

在量子力学中系统的行为用薛定谔方程描述，方程的解称为波函数。系统的完整信息用它的波函数表述，通过波函数可以计算任意可观察量的可能值。在空间给定体积内找到一个电子的概率正比于波函数幅值的平方，因此，粒子的位置分布在波函数所在的体积内。波函数模的平方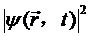代表时刻t、在 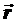处粒子出现的几率密度。物质波是一种几率波，它反映微观粒子运动的统计规律。因此波函数本身并没有直接的物理意义，有物理意义的是波函数模的平方。

 

费米－狄拉克统计和玻色—爱因斯坦统计是在量子力学发展初期建立的。自然界中的微观粒子可以分为两类，费米子和波色子。自旋为半整数（1/2，3/2…）的粒子统称为费米子，服从费米-狄拉克统计，如：质子、中子、电子等。自旋为整数（1，2…）的粒子统称为波色子, 服从玻色-爱因斯坦统计，如光子、介子，以及W和Z粒子。

 

二、费米-狄拉克统计

• 分布和微观状态

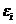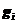设一个孤立系，由N个全同的近独立粒子组成，已知粒子能级，简并度，在能级上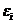上的粒子数为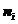，那么N个粒子在能级的分布情况如下：

             能级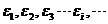   

             简并度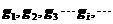  

             粒子数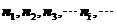  

各个能级的粒子数分别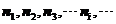为，记为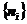称一个分布。分布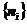决定了系统的宏观性质，对于具有确定粒子数N，体积V和能量E的系统。分布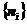必须满足以下条件：

                    , 

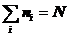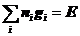
从微观上考虑，在给定一个分布，这个系统可以处于各种不同的微观状态。分布和微观状态是俩个不同的概念。给定一个分布，只能确定每个能级上的粒子数，并不能确定唯一的微观状态。由于单粒子能级通常是简并的，能级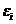上有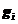个量子态，在给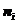定并没有确定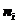个粒子在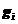个量子态上如何分布。这些都是受泡利不相容原理限制。

对于费米系统，粒子是不可分辨的，粒子在量子态上遵守泡利不相容原理。每个量子态最多能容纳一个粒子，所以对能级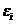必有：

                    

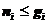
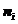个粒子占据能级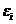上的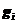个量子态，相当于从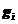个量子态挑选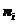个来占据。因此有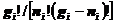种可能方式。各个能级的结果相乘，就得到费米系统的分布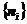相应的微观状态数：

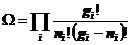                                                 (1)

2．费米分布

根据等概率原理，对处于平衡状态的系统，每个可能的微观状态出现的概率是相等的，因此，微观状态数量的分布，会出现概率最大，称为最概然分布。在理想的条件下，那么费米的最概然分布称为费米分布。

假设系统具有确定的粒子数N，体积V和能量E，分布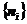同样必须满足以下条件：

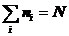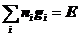                    ,                      (2)

我们引入斯特林公式：   ，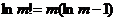

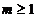
所以对公式（1）进行求导得：

                 

               (3)

假设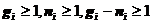  上式（3）可以近似为：

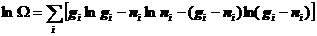                        (4)

为了使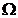为极大值，分布必有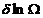=0.同时利用拉格朗日乘子法，引入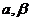俩个乘子，有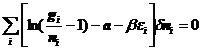          

又因为每个粒子数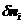都是独立的，因此每个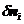的系数都等于零； 

所以                   

得到的费米-狄拉克统计为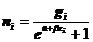：                          (5)

 

三、玻色-爱因斯坦统计

在统计力学中，玻色-爱因斯坦统计确定了在热平衡下同一的不可分辨的玻色子相对于能量状态的统计分布。

假设我们有许多能级，以i来标记，每个能级的能量为ei，包括了全部的ni个粒子。假设每个能级包括了gi个不同的子能级，都有相同的能量，而彼此可分辨。例如，两个粒子有不同的动量，在这种情况下它们是可分辨的，但是它们仍可能有相同的能量。和能级i关联的gi值称为该能级的“简并度”。任意数量的玻色子可以占据同一子能级。

令w(n,g)为n个粒子在一个能级中的g个子能级的分布方法数。对于一个子能级，只有一种分布方法，因此w(n,1)=1。容易看出n个粒子在两个子能级上有n+1种分布方法，我们写成：

                                  

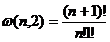
可以看出n个粒子在三个子能级的分布方法数为w(n,3)= w(n,2)+ w(n-1,2)+…+w(0,2)，所以

           

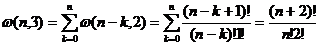
这里我们用到了下面包含二项式系数的定理：

                                 

继续这个过程，我们可以看出w(n,g)就是一个二项式系数

                        

 

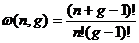
可以看出，对于一系列的占据数ni，方法数为每一个能够填充的单独能级的方法的乘积：

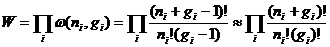                    (1)

两边都取自然对数

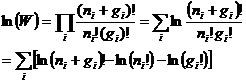                              (2)

根据斯特林近似

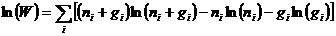                   (3)

又有边界条件

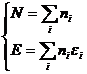                                                  (4)

其中N为系统的总粒子数，E为系统的总能量，ei为每个能级的能量。

根据拉格朗日乘数法，可构造出函数 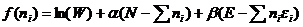                                  (5)

要使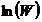的值最大（也就是W的值最大），即要找出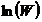的极值对应的ni，可以用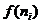的极值来代替，即

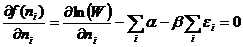                              (6)

按照(3)式，有

            

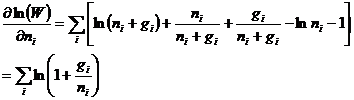
代入(6)得

            

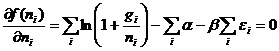
即

                   

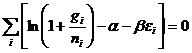
也就是

                     

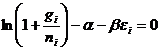
解得费米-狄拉克填充数的ni：

                      

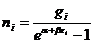
可以证明在热力学中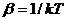，这里k为玻耳兹曼常数T为温度。而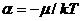，这里为化学势，因此最后得到玻色-爱因斯坦统计为：

                                     

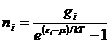
费米-狄拉克和玻色-爱因斯坦统计适用于量子效应必须考虑和粒子被看作是“不可分辨的”情况下。如果粒子的密度N/V³nq（nq为量子密度），量子效应就显现出来。量子密度就是粒子间距等于热德•布罗意波长的时候，即粒子的波函数已经接触但还未重叠时。量子密度依赖于温度；高温会使大多数系统处于经典的限制中，除非它们有非常高的密度比如白矮星。费米-狄拉克统计适用于费米子（服从泡利不相容定律的粒子），玻色-爱因斯坦统计适用于玻色子。在经典极限条件下（高温或低密度）费米-狄拉克和玻色—爱因斯坦统计都变为麦克斯韦—玻耳兹曼统计。