经典统计物理
概率论与数理统计在经典统计物理中的应用
概率论是现代数学的一个重要学科。一方面,他有丰富的数学理论,与其他数学学科有深入的相互渗透。另一方面,它与自然科学、技术科学、管理科学、经济科学以至人文科学有广泛的交叉。很多问题都可以归结为概率模型,应用概率论和随机过程的理论和方法加以研究.并且这些问题也向概率论提出了新的重要研究课题。经典统计物理学便是这样一个新的概率论分支。统计物理学根据对物质微观结构及微观粒子相互作用的认识,用概率统计的方法,对由大量粒子组成的宏观物体的物理性质及宏观规律作出微观解释的理论物理学分支。
下面我们分别以麦克斯韦气体分子速率分布律、麦克斯韦-波尔兹曼统计分布、理想气体的温度公式和压强公式为例,说明概率统计在经典统计物理中的应用。
1. 麦克斯韦气体分子速率分布律
麦克斯韦用概率论证明了在平衡态下,理想气体分子速度分布是有规律的,这个规律叫做麦克斯韦速度分布率,若不考虑分子速度的方向,则叫麦克斯韦速率分布率。
能量为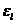 的分子概率密度是
的分子概率密度是
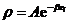 , (1-1)
, (1-1)
其中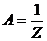 是归一化常数,而分子能量是
是归一化常数,而分子能量是
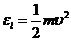 . (1-2)
. (1-2)
由归一化条件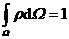 得
得  ,
,
相体积元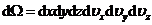 =
= .
.
不失一般性,设气体体积为单位体积,则积分
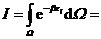
 .
.
利用积分公式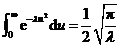 , 得
, 得
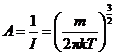 .
.
于是有 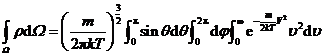
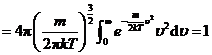 .
.
定义: 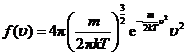 , (1-3)
, (1-3)
则有 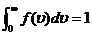 . (1-4)
. (1-4)
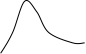
所以,函数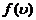 是平衡态理想气体中分子按速率分布的概率密度函数,叫做麦克斯韦气体分子速率分布律(Maxwell distribution law of speed of gas molecules), 表示速率
是平衡态理想气体中分子按速率分布的概率密度函数,叫做麦克斯韦气体分子速率分布律(Maxwell distribution law of speed of gas molecules), 表示速率 附近单位速率间隔内的分子数占气体总分子数的比例. 例如,若气体总分子数为
附近单位速率间隔内的分子数占气体总分子数的比例. 例如,若气体总分子数为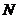 ,则速率
,则速率 附近速率间隔
附近速率间隔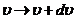 内的分子数是
内的分子数是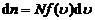 .
.
为简便起见,可将函数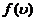 写成
写成
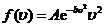 , (1-5)
, (1-5)
其中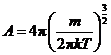 ,
,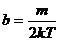 ,其函数曲线如图1所示.
,其函数曲线如图1所示.

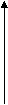





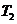

 O
O 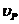
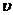 O
O 
图1 图2
除满足归一化条件外,函数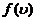 还具有以下特点:
还具有以下特点:
(1) 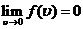 ,
,  ;
;
(2) 令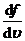 =0, 得最概然速率:
=0, 得最概然速率:
 . (1-6)
. (1-6)
即 是函数
是函数 的最大值,如图1所示.
的最大值,如图1所示.
式中R和µ分别为普适常量和分子的摩尔质量。最概然速率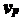 表示对所有的相同速率区间而言,在含有速率
表示对所有的相同速率区间而言,在含有速率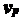 的那个区间内的分子占总分子数的百分比最大。
的那个区间内的分子占总分子数的百分比最大。
(3) 由(1-3) 和 (1-6) 式可知,当气体温度上升时,或用分子质量较小的气体代替分子质量较大的气体做实验,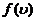 的函数曲线将右移并变得平缓,如图2所示。
的函数曲线将右移并变得平缓,如图2所示。
2. 气体分子的平均速率
我们知道,气体处于平衡态,其分子的速率有大有小,服从Maxwell气体分子速率分布律. 所以,气体分子的平均速率是
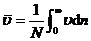 .
.
将 代入上式做分部积分,得
代入上式做分部积分,得
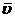 =
= =
=
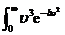
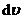 =
=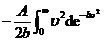 =
=
= =
=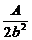 ,
,
即理想气体速率从0到∞整个区间内的算术平均速率为 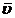 =
=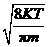 =
= . (2-1)
. (2-1)
3. 物理统计规律之麦克斯韦-波尔兹曼统计分布(M-B分布)
麦克斯韦-波尔兹曼统计分布是研究近独立经典粒子按能量的最概然分布。
设有一个由 个相同粒子组成的系统,其中每个粒子可以被看成一个子系统. 如果粒子之间的相互作用足够弱,则可以忽略它们之间的相互作用能,这样的系统就叫做近独立粒子系统(near independent particle system),而系统的能量
个相同粒子组成的系统,其中每个粒子可以被看成一个子系统. 如果粒子之间的相互作用足够弱,则可以忽略它们之间的相互作用能,这样的系统就叫做近独立粒子系统(near independent particle system),而系统的能量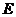 等于每个粒子的能量
等于每个粒子的能量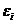 的和:
的和:
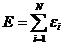 . (3-1)
. (3-1)
在由相同粒子组成的近独立粒子系统中,每个粒子具有相同的子相空间,系统中的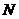 个粒子可以同时用一个子相空间来描述。 这样,在这个子相空间中就同时有
个粒子可以同时用一个子相空间来描述。 这样,在这个子相空间中就同时有 个相点,
个相点, 个相点的一种分布表示系统的一个微观态. 系统有多少可能的微观态,就有多少种分布方式。
个相点的一种分布表示系统的一个微观态. 系统有多少可能的微观态,就有多少种分布方式。
为了计算系统一个宏观态包含的微观态数目,把子相空间中 个相点可能出现的区域划分为
个相点可能出现的区域划分为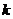 个微小区域:
个微小区域:
 , (3-2)
, (3-2)
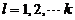 ,划分的原则是同在一个微小区域内的粒子具有近似相等的能量,记作
,划分的原则是同在一个微小区域内的粒子具有近似相等的能量,记作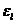 , 一个微小区域
, 一个微小区域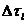 叫做一个相格(phase cell). 假设系统处于某个宏观态时,相格
叫做一个相格(phase cell). 假设系统处于某个宏观态时,相格 内有
内有 个粒子,即粒子数按相格的分布是
个粒子,即粒子数按相格的分布是 =(
=(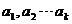 ). 显而易见,粒子数按相格的分布应满足下面的总粒子数和总能量条件:
). 显而易见,粒子数按相格的分布应满足下面的总粒子数和总能量条件:
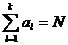 ,
,  . (3-3)
. (3-3)
设相格 内有
内有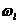 个可供粒子占据的态
个可供粒子占据的态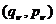 (
( ),即有
),即有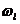 个相点. 由于子相空间中的相点是均匀分布的,相格内每个粒子态占有的相体积
个相点. 由于子相空间中的相点是均匀分布的,相格内每个粒子态占有的相体积 =
=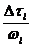 是一个常数. 经典理论对粒子占据微观态没有限制,因此,相格
是一个常数. 经典理论对粒子占据微观态没有限制,因此,相格 内每个粒子可占据的微观态数都是
内每个粒子可占据的微观态数都是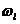 个, 而
个, 而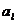 个粒子占据
个粒子占据 个微观态的方式有
个微观态的方式有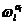 种. 这样,当粒子数按相格的分布
种. 这样,当粒子数按相格的分布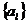 给定时,全部粒子占据微观态的方式共有
给定时,全部粒子占据微观态的方式共有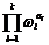 种. 注意,现在只是给定了各个相格中的粒子数,还需要考虑是哪些粒子占据了哪些微观态. 经典理论为粒子是可以分辨的,因此,在给定了各个相格中的粒子数的条件下,粒子的组合数是
种. 注意,现在只是给定了各个相格中的粒子数,还需要考虑是哪些粒子占据了哪些微观态. 经典理论为粒子是可以分辨的,因此,在给定了各个相格中的粒子数的条件下,粒子的组合数是
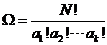 .
.
上式是这样得到的:若不管粒子在哪个相格,全部粒子的排列数是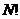 扣除各个相格内粒子的排列数
扣除各个相格内粒子的排列数 ,就得到上式. 所以,当系统处于某个宏观态,即当粒子数按相格的分布
,就得到上式. 所以,当系统处于某个宏观态,即当粒子数按相格的分布 给定时,该宏观态包含的微观态数目是
给定时,该宏观态包含的微观态数目是

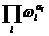
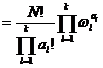 . (3-4)
. (3-4)
(3-4) 式表明,宏观态包含的微观态数目是粒子数按相格的分布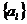 的函数,记作
的函数,记作 . 统计物理学的基本假设是:孤立系统的各个微观态出现的概率相等. 因此,粒子数按相格的最概然分布就是微观态数
. 统计物理学的基本假设是:孤立系统的各个微观态出现的概率相等. 因此,粒子数按相格的最概然分布就是微观态数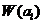 最大的分布. 为求得最概然分布,对(3-4)取对数:
最大的分布. 为求得最概然分布,对(3-4)取对数:
 .
.
为取极大值,令
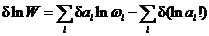 =0. (3-5)
=0. (3-5)
对斯特令公式(Stirling formula) 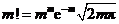 取对数:
取对数:
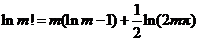 .
.
当 很大时,
很大时,  , 忽略上式最后一项,得
, 忽略上式最后一项,得
 . (3-6)
. (3-6)
利用上式可由 (3-5) 式得
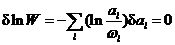 (3-7)
(3-7)
由 (3-3) 式得 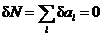 ,
, 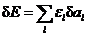 .
.
由于分布 应满足 (2-1-3) 式, 对上两式乘以待定常数
应满足 (2-1-3) 式, 对上两式乘以待定常数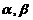 , 并从(3-7)式中减去, 得
, 并从(3-7)式中减去, 得 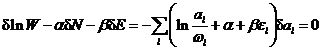 .
.
若要上式成立,必须有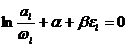 , 即有
, 即有
 . (3-8)
. (3-8)
这就是粒子数按能量的最概然分布,叫做玻尔兹曼分布(Boltzmann distribution),两个待定常数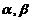 由(3-3)式确定:
由(3-3)式确定:
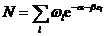 ,
, . (3-9)
. (3-9)
4. 理想气体的温度公式和压强公式
这一节运用统计方法推导两个公式:温度公式(temperature formula)和压强公式(pressure formula),以加深对理想气体和统计方法的理解.
(1) 温度公式
理想气体分子的平均平动能是
 =
=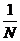
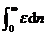 =
=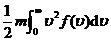 . (4-1)
. (4-1)
将(1-5) 式代入上式,做分部积分,得
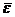 =
=
 . (4-2)
. (4-2)
这叫做温度公式,它表明温度是气体分子热运动平均平动能的量度.这就是温度的微观意义. 上式把温度这个宏观量与气体分子平动能这个微观量的平均值联系了起来,是统计方法的典型体现.
(2) 压强公式
如果气体分子与容器壁碰撞,它的动量将改变,同时给器壁以作用力. 大量分子的密集碰撞就形成了对器壁的压力。按照热力学,理想气体的压强是
 .
.
但是,在热力学中,上式是一个实验结果,其中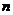 是分子数密度。我们把理想气体看成近独立粒子系统得到了上式。现在运用大量气体分子密集碰撞器壁这个模型来推导上式,出发点是关于理想气体的三条假设。
是分子数密度。我们把理想气体看成近独立粒子系统得到了上式。现在运用大量气体分子密集碰撞器壁这个模型来推导上式,出发点是关于理想气体的三条假设。


 如图 4-1所示,设质量为
如图 4-1所示,设质量为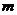 的气体分子以速率
的气体分子以速率
 与器壁发生弹性碰撞,碰撞前后分子动量的增量是
与器壁发生弹性碰撞,碰撞前后分子动量的增量是
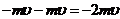 . 图 4-1
. 图 4-1
按照Maxwell 气体分子速率分布律,单位体积中速率在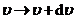 范围内的气体分子数是
范围内的气体分子数是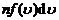 . 由于气体分子向各个方向运动的概率相同,单位体积中速率在
. 由于气体分子向各个方向运动的概率相同,单位体积中速率在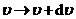 范围内的分子只有
范围内的分子只有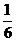
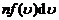 个分子射向图中右边的器壁. 由于分子之间的碰撞是弹性的,碰撞只是使分子交换该方向的速度,对射向器壁的平均分子数无影响,这样,单位时间内与器壁单位面积发生碰撞的分子数目是
个分子射向图中右边的器壁. 由于分子之间的碰撞是弹性的,碰撞只是使分子交换该方向的速度,对射向器壁的平均分子数无影响,这样,单位时间内与器壁单位面积发生碰撞的分子数目是

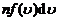 ,碰撞前后这些分子动量的增量是
,碰撞前后这些分子动量的增量是
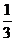
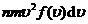 .
.
积分上式,得
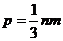
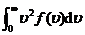
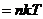

由此可见,物理学家将数学中的统计和概率的方法引入分子物理学,得到了分子运动速度分布率等一系列规律,从而建立了经典统计物理学。