非平衡态统计物理学

非平衡态统计物理学虽然与平衡态统计物理学有着同样悠久的历史，但是直到20世纪中期才逐渐形成一些普遍概念，开始勾划出理论体系。自然界中平衡态是相对的、特殊的、局部和暂时的，不平衡才是绝对的、普遍的、全局和经常的。非平衡现象千姿百态、丰富多彩，短时期内不可能期望建立与平衡态理论媲美的包罗万象的非平衡态统计物理。虽然对于自然界中若干类的非平衡现象，已经建立了普遍的宏观描述和相应的统计理论，然而非平衡态统计物理作为一个整体、仍是一门尚在迅速发展、远未达到成熟阶段的学科。

以下从两个方面介绍非平衡统计物理学的内容和方法。一方面，针对已经能够成功地处理的物理问题，介绍非平衡现象的宏观或半宏观描述，列举主要的定理和结论；另一方面，结合非平衡态统计物理学的主要方法，概述这一理论目前所具有的数学结构，指出理论中存在的一些基本问题。

在稳定的平衡态附近，主要的趋势是趋向平衡。如果对处于平衡态的物理系统施以短暂的小扰动，则取消扰动后，系统经一定时间就要回到平衡，所需的这一段时间称为弛豫时间，这类过程称为弛豫过程。宏观描述中往往引入一个弛豫时间就够了。计算弛豫时间的数值及温度依赖关系等，则是统计理论的课题。 

如果强行维持使物理系统处于不平衡状态的外界条件，例如温度差，浓度差、电位差（可把它们看作是广义力，记作Xi），但又不使其离开平衡太远，则系统内会产生持续不断的“流”Ji。离开平衡不远时，流正比于力。这个正比关系概括了19世纪以来建立的一大批经验规律。例如电流正比于电位差(欧姆电导定律，1826)，热流正比于温度差（傅里叶热传导定律，1822），粒子流正比于浓度差（斐克扩散定律，1855）。这些流描述电荷、能量、质量等等的转移和输运。输运过程中消耗的功率比例于力的二次方。因此，这些过程统称为输运过程或耗散过程。事实上输运过程可以错综复杂地进行。一种力能引起多种流，一种流可来自多种力。例如，温度差不仅直接引起热流，还可以引起扩散流。这就是Ch.索里特在1879年发现的热扩散效应，后来发展成为分离同位素的方法之一。浓度差不仅直接引起扩散流，还能导致热流。这就是L.迪富尔在1872年发现的扩散热。因此，一般情形下应把流和力的关系写成

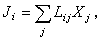                        　                        　　(1)

Lij称为输运系数或线性输运系数。电导率、热导率、扩散率、粘滞系数，热扩散系数等等都是输运系数。由式(1)描述的过程，又称为线性不可逆过程或线性响应。

　　宏观的平衡态对应瞬息万变的微观运动方式，是微观运动的平均表现。因此，各个宏观参数并不是一成不变地等于统计平均值，而是在平均值上下起伏摆动。如果对宏观系统中“微观大、宏观小”的部分作测量，则这些围绕平均值的涨落尤为清楚。涨落的存在，还给出物理仪器的测量精度极限。研究涨落的概率，可以利用玻耳兹曼关系式(16)（爱因斯坦，1910）。涨落时的熵变化与系统中发生此种可逆涨落所需之最小功R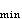有热力学关系ΔS=-R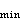/T，于是利用最小功的表达式可以写出涨落的概率

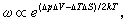                         　　                 　(2)

恰当地选择变量，就可以由式(2)计算各种热力学量的涨落，特别是当体积一定时，能量涨落的均方值是

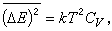                          　                 　　(3)

其中Cv是定容热容；而粒子数涨落的均方值正比于等温压缩率和粒子数密度的二次方

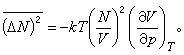                　                  　　(4)

平衡态附近的情形 　

弛豫、输运（耗散）和涨落是平衡态附近的主要非平衡过程。它们都是由趋于平衡这一总的倾向决定的，因而与平衡态有一些深刻的内在联系。例如，系统局部受到短暂的小扰动而离开平衡，或者由于自发的涨落而偏离平衡，其后回到平衡的弛豫过程应是相同的，应由系统的内部性质决定，而与最初偏离平衡的原因无关。因此，涨落和输运系数都可以完全用平衡态的物理量表示出来。

偏离平衡不远的线性不可逆过程的热力学和统计物理，已经是发展成熟的理论，其主要内容由以下三个原理描述。

① 输运系数对称原理(又称昂萨格倒易关系)。当选择流和力的定义之后，式(1)中的输运系数矩阵是对称的

                             Lij＝Lji。                      　　　(5)

如果有外磁场H存在，式(5)应写为

                        Lij(H)＝Lji(-H)，                     　　　(6)

对于角速度为ω的旋转系统，式(56)应写为

                         Lij(ω)＝Lji(-ω)。 　                   　　(7)

1854年W.汤姆孙（即开尔文）研究热电效应时，推导出第一个对称关系。这个原理的一般形式是由L.昂萨格于1931年从微观运动方程在时间反演下的不变性出发证明的。

　　② 涨落耗散定理。输运系数Lij 由相应流Ji和Jj的热涨落决定。1928年H.尼奎斯特证明，线性电路中热噪声电动势的均方值与电阻成正比

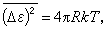                           　                 　　(8)

这就是一个涨落耗散定理，其实早在1905年爱因斯坦得到的布朗运动粒子在时间t内的均方位移与扩散系数D的正比关系

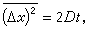                       　                      　　(9)

也是另一种意义下的涨落耗散定理。这个定理的普遍形式是H.B.卡伦和T.A.韦尔顿(1951)证明的。作为它的一个特例，可以导出久保亮五的直流电导率公式

                    　                　　(10)

它把σij这个输运系数通过电流自己的平均关联表示出来。注意式(10)中的平均只须用平衡态的分布函数计算。换言之，涨落耗散定理是说，可以把物理系统的一些非平衡性质通过平衡性质表示出来。 
　　 ③ 最小熵产生原理。不可逆过程使系统的熵增加。熵产生的速率由广义力的二次型决定

                            　　                   　(11)

(此式中dS仅指系统内产生的熵,不包括通过边界与外部交换的熵)。平衡态是一种不随时间变化的定常态。平衡态附近也可能存在另外的一些不随时间变化的定常态。I.普里戈金在1945年证明的最小熵产生原理指出，熵产生p取最小值的态也是定常态,这些定常态区别于其他非平衡态的特点就是熵产生p取最小值。应当指出,这一原理的适用范围比前面两个原理要窄。除了偏离平衡不远这一共同前提外，它还要求下面将要介绍的局域平衡假定成立。最小熵产生原理的物理图像是清楚的：如果外力的存在使系统不能趋近平衡(即p＝0的)态，它就进入p最小的态。

另一大类非平衡现象的宏观描述是在局域平衡假定下建立的。这里又可以区分两种情形。第一种、也是最重要的情形，是物理系统的整体虽然处于非平衡态，但系统中每个微观大、宏观小的部分却近似地处于局部的热平衡态。因此可以定义依赖于空间坐标、甚至随时间缓慢变化的温度、化学势等热力学量，并在每一个局部引用平衡态的热力学关系。这类理论的最成功的例子就是流体力学。它是对于时空坐标的五个函数（流体速度的三个分量、密度和压力）建立的封闭的非线性方程组。 

第二种局域平衡系统通常是空间均匀的，但系统的全部运动自由度可以分成若干个组或者若干个子系统，每个子系统内部由于相互作用较强而迅速达到平衡，但是子系统之间耦合较弱,需要较长时间才能达到平衡。这种情形下，可以为每一个子系统定义各自的温度。例如，晶体中磁性原子的自旋自由度和点阵的振动自由度往往就可以分开处理。

与这种描述密切相关的，是负温度的概念。这最好用一个简单的例子说明。设晶体中掺入N个杂质原子,每个原子具有两个可能的能量状态ε0＝0和ε1，各有n0和n1个原子处于这些状态中:N＝n0+n1。形成这个状态的微观方式共有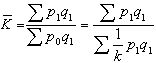种，于是根据式(16)，杂质原子组成的子系统的熵是

S＝klnW＝k(NlnN-n0lnn0-n1lnn1)，

这里使用了斯特令近似公式

lnN!≈NlnN-N。

由于子系统的内能U＝n1ε1，由热力学关系求得

                　　                　(12)

可见当n0＞n1时，温度是正的；n0＝n1时，对应T＝∞；而在“占有数反转”即n0＜n1时,温度成为负数。应当强调指出,负温度只是描述能级数目有限(上面例子中是两个) 的子系统“占有数反转”状态的一种方便的语言，在研究微波量子放大器和激光器时是一个有益的概念。对于热力学系统，可以严格证明温度必须是正值。

　　远离平衡态的情形 　

20世纪60年代以来，对于远离平衡态的物理现象进行了广泛的研究，但是尚未形成完整的理论体系。这里最重要的一类现象是远离平衡的突变，有序与结构的出现。例如，从下面加热夹在两个无穷平板之间的液体。当上下两板之间温度差不大时，只有不伴随宏观流动的热传导过程。温度差达到一定临界数值时，突然出现规整的对流花纹。这是一类非平衡的相变现象，与平衡态的相变有许多相似之处。第一，通常有某个参数达到一定阈值，新状态才突然出现，这是一种临界现象。第二，新状态具有更丰富的时间和空间结构，例如周期行为或花纹图样。第三，只有不断从外界提供能量，这些结构才能存在下去。第四，新结构一旦出现，就具有和平衡态类似的稳定性，不易因外界条件的微小改变而消失。普里戈金等在1969年建议以耗散结构一词概括这类现象。宏观量之间的非线性关系，在远离平衡时有重要作用。耗散结构的理论，主要基于非线性方程的分叉点分析，基本上处于宏观描述阶段。 

主要研究方法 　统计物理学所面临的数学问题，介于动力系统（多自由度乃至无穷自由度的力学）理论和概率论与随机过程理论之间。非平衡统计物理学的主要方法，也是左右逢源，可以划分为两大类。

第一类是从微观力学出发的统计理论，可以概括为“刘维方程加统计假定”。刘维方程式(20)，可改写成算符形式

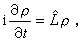                         　                      　　(13)

其中刘维算符怉在经典情形下就是泊松括号

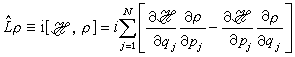         ，          　　　(14)

而在量子情形下则是哈密顿算符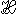和密度矩阵孨 的对易子。量子力学中式(13)有时称为冯·诺埃曼方程。通称之为刘维方程。

彻底的非平衡统计物理学,应当从刘维方程出发,加上明确的统计假定，导出各种宏观和半宏观描述，并在它们不适用的情形下，提供直接的统计处理方法。然而对于非平衡统计假定的认识，目前远不如平衡态的基本统计假定。这里只能略作介绍。

把N点分布函数ρ对N-1、N-2、…个变量积分之后，定义单点、两点、……等等约化分布函数

                   　　                     　(15)

由刘维方程出发，可以为这些约化分布函数推得无穷个耦合方程,其中ρK的方程中出现ρK+1等等。此即经典或量子的BBGKY(Bogoliubov-Born-Green-Kirkwood-Yvon)方程链。任何较为实际的讨论，都需要把这个方程链截断，将ρK通过前面的ρK-1、ρK-2等等表示出来,以获得一个封闭的方程组。这类“截断近似”通常隐含地对应某种统计假定,其意义往往不很清楚。比较成功的例子,是H.H.博戈留博夫于1946年在两条假定下比较严格地推得了经典的玻耳兹曼输运方程(11)。这两条假定是：①两点分布函数可以表示为单点函数的泛函ρ2=ρ2【ρ1】,②在t→-∞并取热力学极限(N→∞,V→∞,N/V有限)之后二体关联衰减而有

                        　　              　(16)

玻耳兹曼方程还可以在其他一些大同小异的假定下推导出来。 
　　 对于量子情形,早在1928年W.泡利就为密度矩阵孨的对角元素推导得如下的主方程(master equation)

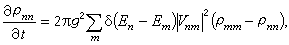                           (17)

其中g 是耦合常数，Vmn是相互作用势的矩阵元。这个方程可以描述趋近平衡的不可逆过程，但推导中每一步都要使用无规相位近似，即舍去密度矩阵的非对角元素。后来L.C.P.范霍甫(1957)和普里戈金(1961)只在初始时刻使用一次无规相位近似，推得了形式有所不同的主方程，并且讨论了趋向平衡的条件，说明不可逆性与热力学极限中的无穷体积有关。

　　非平衡统计物理学中的第二类方法，直接从随机方程出发，因而不需要统计假定，却带上了更多的半唯象描述的成分。20世纪初期P.朗之万在布朗粒子的牛顿运动方程中加上了随机力ξ(t)

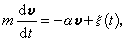                        　　                 　(18)

用来反映没有归纳到摩擦力αv中去的其他运动自由度的影响。这是首次在物理学中使用随机微分方程，因此这一类方程以后统称为朗之万方程。现代非平衡统计物理中的朗之万方程可以表述如下。选择宏观变量的集合{Qi,i＝1,2,…n}来描述某一类非平衡现象,它们遵从广义的朗之万方程组

              　　               　(19)

其中势函数 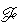 在平衡态附近就是自由能，而在某些远离平衡的定常态附近也可以从微观运动方程的时间反演对称出发，证明存在着类似的势函数。对称矩阵描述宏观变量 Qi 的耗散和扩散运动，保证系统能够趋向平衡。Ki(Q) 反映不能通过势函数表示出来的宏观变量之间的耦合，例如当Qi代表平均磁矩时，磁矩的进动项就包含在Ki(Q)之中。这一项通常称为模模耦合,每个Qi就是一个运动模。关于随机力i(t),通常假定它遵从高斯分布，且

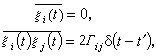                       　                 　　(20)

式(20)中出现的Γij就是方程(19)中的，这才能保证t→∞时Qi趋近由势函数 最小值决定的定常态。式 (20)是另一种意义下的涨落耗散定理。

　　朗之万方程可以看作从随机过程 {ξi(t)}到随机过程{Qi(t)}的变换。对于Qi的概率分布函数p(Q,t),可从朗之万方程(19)推导出如下的福克-普朗克方程

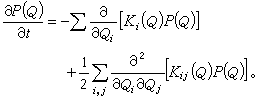              　　            　　(21)

这是{Qi}空间中的推广的扩散方程，等号右端第一项是漂移项，第二项是扩散项。相反，从每一个福克－普朗克方程，可以推导出一批随机等价的，即遵从同一种随机分布的朗之万方程。关于朗之万方程和福克－普朗克方程的关系和性质，可参看随机过程和随机微分方程的有关条目。 

　　以上处理非平衡统计问题的两类方法，并不是互相对立或无关的。事实上,线性不可逆过程的统计理论,可以同样好地应用这两套方法来建立。用由微观力学出发的确定论的方法，论证和推导概率论的理论形式，已经有过一些富有意义的尝试。