熵的统计解释和H定理

热力学中另一个重要的概念是克劳修斯在1865年引入的熵。熵是物理系统状态的一个函数。对于孤立系统,它的数值永不减少;系统中进行可逆过程，熵的数值不变；而不可逆过程使熵的数值增加；平衡态对应熵的最大值。熵的统计解释主要是奥地利物理学家L.玻耳兹曼的贡献。玻耳兹曼的工作说明了用统计考虑可以为热力学奠定基础，同时也开创了不可逆过程的研究。 

和麦克斯韦一样，玻耳兹曼不是考虑单个分子的运动，而是引入分布函数 f(r,v,t)，使f(r,v,t)drdv代表速度在 v和v+dv，坐标在r和r+dr范围内的分子数目。显然与式(5)类似，应有

　　　

其中N是分子的总数。

　　分布函数f(r,v,t)随时间的变化由两部分原因引起：一是分子的坐标和速度按力学运动方程的变化，即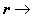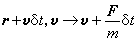(F是作用在分子上的力,故F/m是加速度);二是分子间相互作用(碰撞)引起的改变。前者是运动状态的连续变化，经过 δt时间之后，原处在drdv范围内的分子, 全部进入对应dr┡dv┡的状态，数目并没有增减。后者（碰撞）则使得一些分子进入drdv, 而另一些分子离开这一范围，其净效果用碰撞项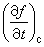表示。于是

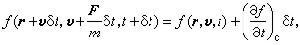
或对δt展开，得到

　　　

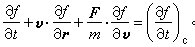
　　具体的碰撞项只有根据分子间相互作用的具体模型和一些补充假定才能推导出来。在只计入二体碰撞和认为分子的速度与位置没有关联(“分子混沌性”假设)的条件下，玻耳兹曼求得如下的碰撞积分

　

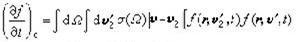
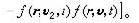
这个式子中 σ(Ω )是在立体角Ω 内的碰撞截面，v、v2和v┡、v娦 是两个分子在碰撞前后所具有的速度。式(11)和(12)合在一起，构成玻耳兹曼输运方程。这是关于函数f(r，v,t)的一个非线性积分微分方程。麦克斯韦速度分布律(7)是这个方程的一个均匀（不含r）定常态（与t无关）解。 

对于输运方程的任何一个解，玻耳兹曼在1872年定义了如下的H量

　　　

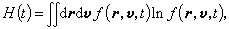
并且证明了它是一个不随时间上升的量，即

　　　

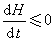
这就是玻耳兹曼的H定理。式(14)中等号成立的条件,是碰撞积分式(12)等于零，即碰撞前后的分布函数满足

　　　

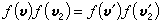
这个式子可以从左右两面读，说明正反两种碰撞过程的作用相抵。这叫作细致平衡条件。这个条件成立时，分布函数不因分子碰撞发生改变，气体达到热平衡。可以证明,满足细致平衡条件的f(v)就是麦克斯韦分布(7)式。显然,细致平衡是维持总平衡的条件。在H定理成立的前提下，细致平衡也是维持总平衡的充分和必要条件。总平衡能否由不同于细致平衡的其他条件维持，是目前尚未完全解决的问题。 
　　 除了平衡分布以外，其他情形下H(t)都随时间下降。因此,－H具有热力学熵的基本性质。然而，这还不是从微观原理出发，用统计方法定义了熵，因为作为出发点的输运方程本身包含若干假定。H 定理在历史上对于理解宏观系统中不可逆性的来源和趋近平衡的过程，起过重要作用。 
　　 为了说明熵的统计意义，玻耳兹曼还引入了热力学概率W的概念。W实质上不是概率，而是对应同一个宏观状态的微观状态的总数。玻耳兹曼证明，两个热力学状态的熵差正比例于它们的热力学概率的对数之差

S2-S1＝k(lnW2-lnW1)

后来普朗克把这个式子写成

S＝klnW　　　

k是前面已经说明的玻耳兹曼常数。上式有时称为玻耳兹曼关系，它同时规定了熵的绝对数值。只有基于微观量子态的概念，上式的涵义才是完全清楚的。熵的统计定义式并不限于平衡态，它还可以推广到非平衡态。