| |
|
在众多国家中,到底是谁先发现了勾股定理呢?关于这个问题,我们可以自豪地说:“是中国先 |
| |
发现的。”其实,在中国、希腊、埃及这些文明古国虽然处于不同的地区,但却都是很早地、独立地 |
| |
发现了勾股定理,可是为什么中国是最早发现的呢?那案就在《周髀算经》中的记载。《周髀算经》 |
| |
一开始,就记载了我国周朝初年的大政治家周公旦与当时的数学家商高的一段话。在这段话中,周公 |
| |
和商高讨论就是关于直角三角形的一些问题,而且还说到了“勾三股四弦五”的问题。 |
| |
|
周公问商高:“我听说您很精通于数,请问数是从哪里来的呢?” |
| |
|
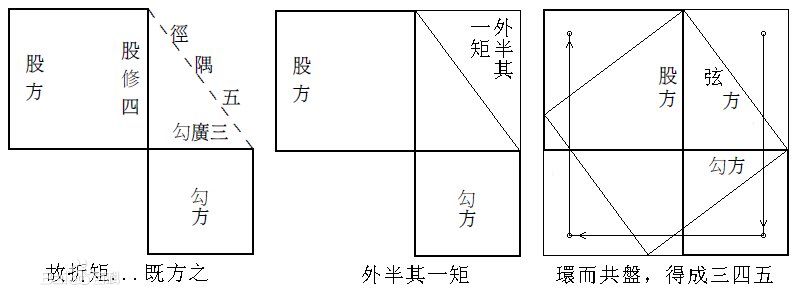
商高回答说:“数的艺术是从研究圆形和方形中开始的,圆形是由方形产生的,而方形是由折成 |
| |
直角的矩尺产生的。在研究矩形前需要知道九九口诀,设想把一个矩形沿对角线切开,使得短直角边 |
| |
(勾)的长度为3,长直角边(股)的长度为4,斜边(弦)长则为5,并用四个上述直角三角形一样 |
| |
的半矩形把它围起来拼成一个方形盘,从它的总面积49中减去由勾股弦均分别为3、4、5的四个直角 |
| |
三角形构成的两个矩形的面积24,便得到最初所作正方形的面积25,这种方法称为‘积矩’。” |
| |
|
在这段讨论中,商高的“勾三股四弦五”就已经具备了勾股定理的所有条件。而毕达哥拉斯所发 |
| |
现“勾股定理”的年代比周朝商高的要晚,所以我国的数学家商高是最早发现勾股定理的人。而“勾 |
| |
股定理”一开始也叫“勾股弦定理”,而这个名字更形象的说明了定理的具体内容。 |
| |
(注:以上拓展共享资源均来自互联网) |