| |
|
托尔斯泰,是俄罗斯最伟大的作家之一,是世界著名的文学家。但他并不是喜欢文学,他对数学 |
| |
也非常的喜欢,而且还提过很多有趣的数学问题。“巴霍姆的故事”是一篇文章里的故事。 |
| |
|
故事的内容为巴霍姆想买一块地,见到了一位酋长,就询问地的价钱。酋长说:“我们的价钱是 |
| |
统一的,每天1000卢布。” |
| |
|
“每天?土地怎么可能用“天”来丈量?“巴霍姆以为自己听错了。 |
| |
|
当然,我们出卖是论天卖的,你一天能多少地方,那些地方就都归你了,无论你走多少,价钱都 |
| |
是1000卢布。但有一个条件,那就是你不能在日落之有回到出发点,你的钱就白花了。”酋长说道。 |
| |
|
巴霍姆想只要自己走得够快,走得够多,就一定可以得到更多的土地,于是他愉快地答应了酋长 |
| |
的要求。他于酋长约定,第二天早上从太阳升起时算起,自己开始走,只要太阳下山以前回到出发的 |
| |
地点,那么,所走的地方就都归他了。第二天天不亮,巴霍姆和酋长来到了草原上的一个土丘旁。酋 |
| |
长摘下自己的帽子,扔在地上,说:“这就是记号,你从这儿走出去,还得走回这儿来。能走多少, |
| |
围出的土地就给你多少。”太阳刚刚升起,巴霍姆就扛起耙子出发了。 |
| |
|
他健步如飞,一口气走出了5俄里,他抬头看了看太阳,大概到了吃早饭的时候。但他想:“先不 |
| |
忙拐弯,再走5俄里吧。”于是他又往前走了5俄里,觉得这一边走得差不多了,于是向左边拐去。在 |
| |
这面也走了很多路,他又拐了第二个弯。走了一阵,巴霍姆看看太阳,已经是中午,第三条边只走了 |
| |
2俄里,而到出发点还要走15俄里。巴霍姆想:“该往回走了,不然日落前就赶不到出发的地方了!” |
| |
他便一直向土丘走去,这时他已经很累了,但是仍然不能停下,他跑了起来,终于,在日落前的一霎 |
| |
那,他跑回了土丘,他终于看到了那个狐皮帽子,他用尽最后的力气,向前扑倒,两手刚好够到了帽 |
| |
子。只是很可惜他并没有得到他所走出的土地,为什么呢?因为他已经累死了。 |
| |
|
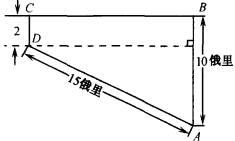
那大家知道不知道巴霍姆走出了多少土地?从故事中,我们就可以知道他走了一个四边形。第一 |
| |
条边是5+5=10俄里。第二条边和第一条边互成直角,但是没有给出长度,我们可以设为X俄里。第三 |
| |
条边为2俄里,第四条边为15俄里,从这些条件我们可以知道巴霍姆从A,到B,到C,再到D,最后回到 |
| |
A,走了一个直角梯形。如果我们知道BC边的长度,就可以算出整个直角梯形的面积。根据勾股定理, |
| |
得出DE=12.69俄里,那么梯形ABCD的面积S=12.69×2+1/2×12.69×8=76.14(平方俄里)。那 |
| |
么巴霍姆走过的总路程也能求出,是10+12.69+2+15=39.69(俄里),约等于40俄里。其实, |
| |
巴霍姆走出的40俄里,如果合理,那么还可以走出更大的一块面积,为什么? |
| |
|
我们知道,周长是在四边形之中的,而且正方形的面积是最大的。如果巴霍姆走出一个边长各为 |
| |
10俄里的正方形的话,那么他走出土地的面积则为10×10=100(平方俄里),比他所走出的要多出 |
| |
24平方俄里。走到累死,但没有获得最多土地,巴霍姆还真是可怜啊!如果他稍微懂些数学,也不会 |
| |
这么冤枉吧! |
| |
(注:以上拓展共享资源均来自互联网) |