| |
|
虽然在几何数学中,各种各样的问题都得到了解决,但至今为止还有三个几何题没能得到解答, |
| |
被称为几何三大难题。那究竟是那几个问题呢,我们一起来了解一下吧! |
| |
|
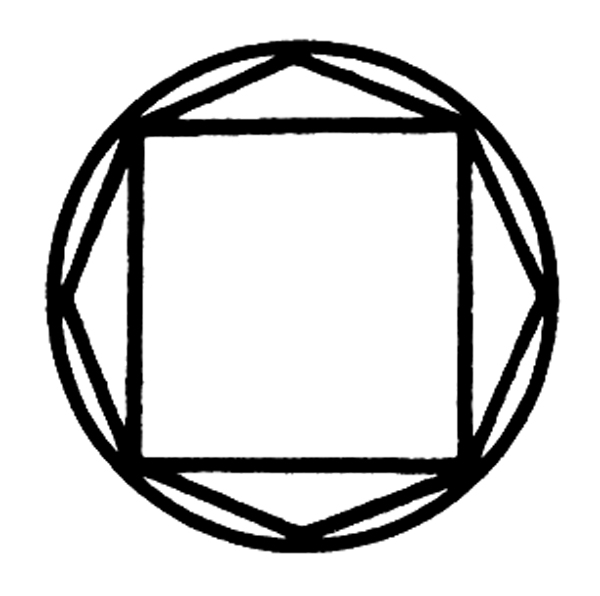
第一,化圆为方。 |
| |
|
在古希腊的时候有一个学者叫做安拉克萨哥拉,有一次,他提出太阳是一个巨大的火球。从现在 |
| |
看来,它绝对符合客观事实,但在当时,人们都相信神话中的说法,太阳是神灵阿巴罗的化身。于是 |
| |
安拉克萨哥拉被判定为亵渎神灵,判处死刑,被投到了牢狱中。 |
| |
|
在等待执行的日子里,他依然在思考关于宇宙和万物的问题,当然也包括数学问题。一天晚上, |
| |
他看到圆圆的月亮,透过正方形的铁窗照进牢房,他心中一动,想:如果已知一个圆的面积,那么, |
| |
怎样做出一个方来,才能使它的面积恰好等于这个圆的面积呢?这个问题看似简单,却难住了安拉克 |
| |
萨哥拉。在古希腊,对作图工具进行了限制,只允许使用直尺和圆规。 |
| |
|
安拉克萨哥拉一直在思考这个问题,甚至忘了自己是还是一个待处决的犯人。到了后来,受到好 |
| |
朋友伯利克里(当时杰出的政治家)的营救,脱离了牢狱之苦。然而这个问题,他自己没有能够解决, |
| |
整个古希腊的数学家也没有能解决,成为历史上有名的三大几何难题之一。在之后的两千多年里,也 |
| |
有无数的数学对此做了论证,可始终没有得到答案。 |
| |
|
第二,立方倍积。 |
| |
|
此问题也是几何三大难题中的一个。相传,在古希腊的有一个名为第罗斯的小岛有一年发生了瘟 |
| |
疫,岛上的居民到神庙去祈求宙斯神,询问该如何免除灾难?许多天过去了,巫师终于传达了神灵的 |
| |
旨意,原来是宙斯认为人们对他不够虔诚,他的祭坛太小了。要想免除瘟疫,必须做一个体积是这个 |
| |
祭坛两倍的新祭坛才行,而且不许改变立方体的形状。于是人们赶紧量好尺寸,把祭坛的长、宽、高 |
| |
都增加了一倍,第二天,把它奉献在了宙斯神的面前。不料,瘟疫非但没有停止,反而更加流行了。 |
| |
第罗斯岛的人民惊慌失措了,再次向宙斯神祈求。巫师再次传达了宙斯的旨意。原来新祭坛的体积不 |
| |
是原来祭坛的两倍,而是八倍,宙斯认为,第罗斯人抗拒了他的意志,因此更加发怒了。当然这只是 |
| |
个传说,但这个问题至今为止都没能解答出来确是事实。 |
| |
|
其问题就是:仅仅用圆规和没有刻度的直尺来做一个立方体,使得这个立方体是已知原来的立方 |
| |
体体积的2倍。由于至今没有人解答,所以它成为了几何学的第二大问题。 |
| |
|
第三,三等分角。 |
| |
|
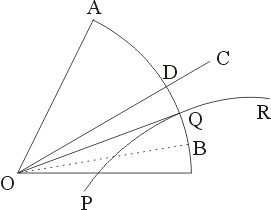
这个问题也有一个传说。据说,在公元前4世纪的时候埃及的亚历山大城是一座著名的繁荣都城。 |
| |
在城的近郊有一座圆形的别墅,里面住着一位公主。圆形别墅的中间有一条河,公主居住的屋子正好 |
| |
建在圆心处。别墅的南北墙各开了一个门,河上建有一座桥。桥的位置和北门、南门恰好在一条直线 |
| |
上。国王每天赐给公主的物品,从北门送进,先放到位于南门的仓库,然后公主再派人从南门取回居 |
| |
室。从北门到公主的屋子,和从北门到桥,两段路恰好是一样长。公主还有一个妹妹小公主,国王也 |
| |
要为她修建一座别墅。而小公主提出,自己的别墅也要修得和姐姐的一模一样。小公主的别墅很快 |
| |
动工了。可是工匠们把南门建好后,要确定桥和北门的位置的时候,却发现了一个问题:怎样才能使 |
| |
北门到居室、北门到桥的距离一样远呢?最终工匠们发现,要想要相等的距离,就必需先要解决三等 |
| |
分的这个问题,只要问题可以解决,就能确定桥和北门的位置。 |
| |
|
于是工匠们尝试用直尺和圆规作图法定出桥的位置,但过了很久,都没有得到解决,无奈之下, |
| |
他们只好去请教当时最著名的数学家阿基米德。阿基米德看到这个问题,想了很久。他在直尺上做上 |
| |
了一点固定的标记,便轻松地解决了这一问题。大家都非常佩服他。不过阿基米德却说,这个问题没 |
| |
有被真正地解决。因为一旦在直尺上作了标记,等于就是为它做了刻度,这在尺规作图法中是不允许 |
| |
的。于是这个问题在两千年来一直困扰着无数的数学家,直到一百多年前,德国数学家克莱因做出了 |
| |
一个无可置疑的证明:只用直尺和圆规,是不可能解决这三个难题的。也就是说,这个问题到目前为 |
| |
止都还没有得到真正的解决。 |
| |
(注:以上拓展共享资源均来自互联网) |