案例20: 0—1背包问题
背包问题在现实生活中有着广泛的应用背景,如预算控制、项目选择、材料切割、货物装载等问题。如果对每个对象只提供两种选择:全部接受或全部拒绝,则该背包问题就是0—1背包问题。
假定一个旅行爱好者准备带着一个背包去旅行。进一步假定旅行者知道背包所能承受的最大负荷为W ,以及他想要携带的n个不同的有用物品集,如帐篷、水壶、压缩饼干、洗漱用品等,每个物品要么全部接受,要么全部拒绝。假设每个物品i由两个值来表征:一个是重量值 Wi一个是旅行者赋予物品的有Pi,他的问题就是在不超过背包载重量W 的前提下,优化所能携带的物品的总价值P,该问题是0—1背包问题的一个典型实例。
解向量可以表示成X={(X0 ,X1 ,……Xn-1)|Xi =0或Xi=1。若n=3,则此0—1背包问题的解空间为{(0,0,0),(0,0,1),(0,1,0),(0,1,1),(1,0,0),(1,0,1),(1,1,0),(1,1,1)}。
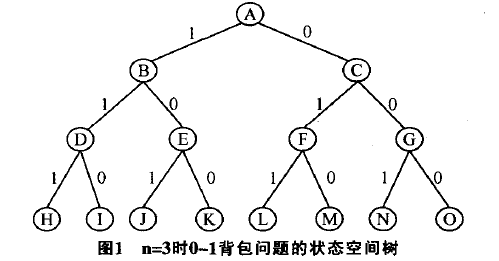
可以用树的形式将解空间表达出来。树中从第i层到第i+1层的边上的值表示解向量中耽的取值,并假定第 层的左子树描述物品 被装入背包的情况,右子树描述物品 被拒绝的情况。则该0—1背包问题的状态空间树就表示为一棵高度为n的完全二叉树。从根结点到叶子结点的任一路径就对应解空间中的一个解向量。
构造出问题的状态空间树以后,就可以从其根结点出发搜索解空间,即决定每个物品的取舍。为了使目标函数的值增加最快,可以优先选择价值最大的物品装入背包,然后是价值量次之的物品⋯⋯直至背包装不下为止。但是,如果所选择的物品重量很大,使得背包载重量消耗速度太快,以至后续能装入背包的物品迅速减少,使得继续装入背包的物品在满足了约束方程的要求以后,无法达到目标函数的要求。因此,最好优先选择那些既能使目标函数的值增加最快。又能使背包载重量消耗速度较慢的物品装入背包。为了达到这个目的,首先把所有物品按价值重量比的非增顺序排列,然后按照这个顺序进行搜索。
在装包过程中,要尽量优先选择价值重量比较高的物品装入背包。表现在搜索过程中,就是要尽量沿着左子树结点前进。当不能继续前进时(假设该结点为T),就得到问题的一个部分解,并把搜索转移到右子树。估计由该部分解所能得到的最大价值,即结点T的上限。可以用贪婪算法处理剩余物品:将按照价值重量比非增顺序排列的剩余物品依次装入背包.至无法完全装入下一个物品时,就将该物品的一部分装满背包。这样就可以得到一个上限。如果该值为当前最优值:继续由右子树向下搜索,扩大部分解,直至找到可行解;保存可行解,并把可行解的值作为当前最优值,向上回溯,寻找其他可行解;若该值小于当前最优值:丢弃当前正在搜索的部分解,向上回溯。反复使
用此方法,直至搜索完整个解空间。
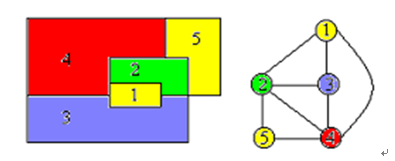
案例21: 图的着色问题是由地图的着色问题引申而来的:用m种颜色为地图着色,使得地图上的每一个区域着一种颜色,且相邻区域颜色不同。问题处理:如果把每一个区域收缩为一个顶点,把相邻两个区域用一条边相连接,就可以把一个区域图抽象为一个平面图。例如,(a)所示的区域图可抽象为(b)所表示的平面图。19世纪50年代,英国学者提出了任何地图都可以4中颜色来着色的4色猜想问题。过了100多年,这个问题才由美国学者在计算机上予以证明,这就是著名的四色定理。例如,在图(b)中,区域用城市名表示,颜色用数字表示,则图中表示了不同区域的不同着色问题 。
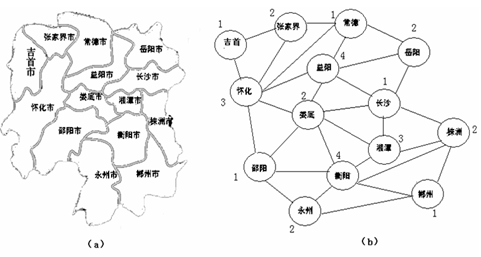
a) 给定无环图G=(V,E),用m种颜色为图中的每条边着色,要求每条边着一种颜色,并使相邻两条边有着不同的颜色,这个问题称为图的边着色问题。
b) 给定无向图G=(V,E),用m种颜色为图中的每个顶点着色,要求每个顶点着一种颜色,并使相邻两顶点之间有着不同的颜色,这个问题称为图的顶着色问题。
给定无向连通图G和m种不同的颜色。用这些颜色为图G的各顶点着色,每个顶点着一种颜色。是否有一种着色法使G中每条边的2个顶点着不同颜色。这个问题是图的m可着色判定问题。若一个图最少需要m种颜色才能使图中每条边连接的2个顶点着不同颜色,则称这个数m为该图的色数。求一个图的色数m的问题称为图的m可着色优化问题。四色问题是m图着色问题的一个特例,根据四色原理,证明平面或球面上的任何地图的所有区域都至多可用四种、颜色来着色,并使任何两个有一段公共边界的相邻区域没有相同的颜色。这个问题可转换成对一平面图的4-着色判定问题(平面图是一个能画于平面上而边无任何交叉的图)。将地图的每个区域变成一个结点,若两个区域相邻,则相应的结点用一条边连接起来。多年来,虽然已证明用5种颜色足以对任一幅地图着色,但是一直找不到一定要求多于4种颜色的地图。直到1976年这个问题才由爱普尔,黑肯和考西利用电子计算机的帮助得以解决。他们证明了4种颜色足以对任何地图着色。