案例22:哥尼斯堡七桥问题
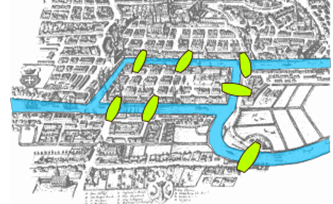
当时东普鲁士可逆斯堡(今日俄罗斯加里宁格勒)市市区夸戈尼亚河中心有两个小岛。小岛与河的两岸有七条桥连接。在所有桥都只能走一遍的前提下,如何才能把这个地方所有的桥都走遍?
当时的欧洲有一座风景秀丽的哥尼斯堡城(即今俄罗斯的加里宁格勒市),这座城市建立在普雷格尔河畔,由4块分开的区域——北区、岛区、南区和东区组成,中间有7座桥相连(如如下图所示)岛上有古老的哥尼斯堡大学,哥尼斯堡大学的学生们经常沿河过桥散步。在散步的过程中,爱动脑筋的人们提出了一个问题:一个散步者能否一次走遍7座桥,而且每座桥只许通过一次,最后仍回到起始地点?

也就是说,可以把每块陆地缩成一个点来看待,我们用A、B、C、D来表示这4个点。 而7座必须经过的桥就是这4个点之间的7条连接线,这种连接线的长短与曲直也与解决问题无关。
“哥尼斯堡七桥问题”就转化为:
“从A、B、C、D中的任一点出发,能否既不重复也不遗漏地把每一条线都走过一遍,并最终回到起点”。这实际上是一个“一笔画问题”,即“能否笔不离纸地一次性画完一个图形并回到起点,而且笔所走过的路线不能重复”
欧拉定理的解释:
⒈凡是由偶点组成的连通图,一定可以一笔画成。画时可以把任一偶点为起点,最后一定能以这个点为终点画完此图。
⒉凡是只有两个奇点的连通图(其余都为偶点),一定可以一笔画成。画时必须把一个奇点为起点,另一个奇点终点。
⒊其他情况的图都不能一笔画出。奇点数除以二便可算出此图需几笔画成。
欧拉就显示出其作为数学家的超常思维。当人们把注意力放在桥、陆地等现实因素并一次次地实地尝试时,欧拉能够抛开陆地的形状、大小、行走路线的长短、曲直等与解决问题无关的因素,抓住该问题中最为本质、最为核心的要素,把实际问题抽象为合适的“数学模型”。这样的“数学化”过程,恰恰是数学探索中最为关键的一点。
如今,图论在解决运筹学、网络理论、信息论、控制论、博弈论及计算机科学等各个领域的问题时,发挥出越来越重要的作用。
图论中的“图”并不仅仅是指几何中的图,而可泛指现实生活、生产活动以及科学研究中各种事物之间的关系。用点表示事物,用点之间的连线表示事物之间的某种关系,这样,点与点之间的若干条连线就构成了图。
事实上,任何一个包含了某种二元关系的系统都可以用图来模拟。研究图的基本概念、性质及应用,构成了图论的主要内容。
欧拉就显示出其作为数学家的抽象思维。
当人们把注意力放在桥、陆地等现实因素并一次次地实地尝试时,欧拉能够抛开陆地的形状、大小、行走路线的长短、曲直等与解决问题无关的因素,抓住该问题中最为本质、最为核心的要素,把实际问题抽象为合适的“模型”。
这样的“抽象化”过程,恰恰是问题求解中最为关键的一点。