回溯法
案例18:八皇后问题:八皇后问题是一个经典的用回溯法来求解的问题。它要求在一个8*8的棋盘上放上8个皇后,使得每一个皇后既攻击不到另外七个皇后,也不被另外七个皇后所攻击。故八皇后问题即:求八皇后的某种布局,使得任意两个皇后不在同一行、同一列或同一斜线上。

假定变量L1、L2、……L8表示在棋盘第一行至第八行中棋子的位置。显然每个变量的取值范围是1~8,任一组合(L1、L2、……L8)都代表一种摆法,它们必须不同行,但它们可以同列或同一对角线,在回溯法中,需要用递归的方法依次确定L1、L2、……L8,在确定Li的取值时,依次尝试Li取1到8,若当前Li的取有值与已确定的L1~Li-1有冲突,则舍弃当前的Li 的值,换一个再次尝试,若1~8全部取遍仍无法得到合法的位置,则 说明当前的变量Li-1的当前取法不当,应退回行,测试Li-1的下一个值。
回溯法的基本思想
首先确定问题的解空间结构,然后按深度优先策略,从根结点出发搜索解空间树。算法搜索至解空间树的任一点时,总是先判断该结点是否肯定不包含问题的解。如果肯定不包含,则跳过对以该结点为根的子树的系统搜索,逐层向其祖先结点回溯;否则,进入该子树,继续按深度优先的策略进行搜索。这种以深度优先的方式系统地搜索问题的解的算法称为回溯法,它适用于求解一些解空间较大的问题。
回溯法的一般步骤
1.针对所给问题,定义问题的解空间。
2.确定易于搜索的解空间结构。
3.以深度优先的方式搜索解空间,并且在搜索过程中用剪枝函数避免无效搜索。
在搜索过程中,通常采用两种策略避免无效搜索:一是用约束函数剪去得不到可行解的子树;二是用限界函数剪去得不到最优解的子树。这两类函数统称为剪枝函数。
回溯算法的一个显著的特性是在搜索过程中动态产生问题的解空间。在任何时刻,只保存从根结点到当前扩展结点的路径。因此,回溯算法的空间需求为0(n),(n为从根结点起最长路径的长度)。而显式地存储整个解空间则需要0(2n )或0(n!)内存空间。
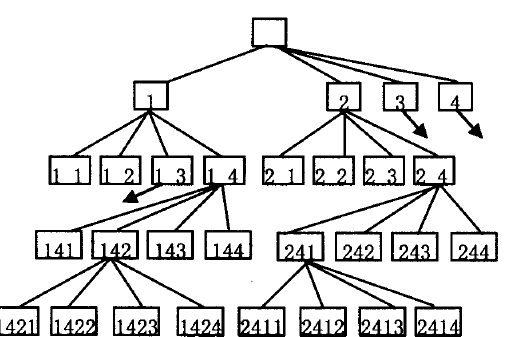
四皇后的解空间数
案例19:迷宫求解问题
迷宫实验是取自心理学的一个古典实验.在该实验中,把一只老鼠从一个无顶大盒子放入,在盒中设立了许多墙,对行进方向形成了多处阻挡.盒子仅有一个出口处放置一快奶酪,吸引老鼠在迷宫中寻找道路以到达出口.对同一老鼠重复进行上述实验,一直到老鼠从入口到出口,而不走错一步.老鼠经多次试验终于得到它学习走通迷宫的线路.设计一个计算机程序对任意设定的迷宫,求出一条从入口到出口的通路,或得出没有通路的结论. 如下图所示,求出一条从入口到出口的通路,或者求出没有通路的结论。

首先考察其解空间的情况。显然,从迷宫的某处出发可以有右、下、左、上四个探视方向。如果迷宫没有没有边界、没有墙壁、且可以重复进入某位置,则以出发点为树根,向右、下、左、上四个位置试探作为向下的分支,且到达每个位置均如此处理。则可以画出一棵无限大的、每个点有4个孩子结点的解空间树,用回溯求解这一问题,就是利用搜索过程中不能出界、不能碰壁、不能重复进入某个方格的约束条件,搜索一条两个方格之间的简单路径。与8皇后问题不同的是,在本问题的递归回溯过程中,并不知道要递归调用多少层就能得到答案,而以达到方格B作为程序结束条件。
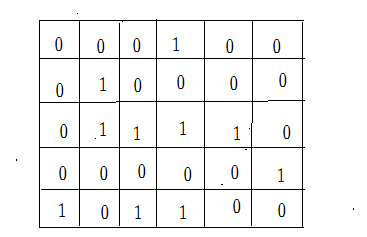
在具体实现中,可将迷宫用二维数组存储,以0、1分别代表迷宫中的通路和障碍,下图所示,然后用递归用递归回溯的方式,,从A位置出发,搜索一条到达B的的通路。
每次到达一个位置后,先将其纳入当前路径;这时,若右侧相邻位置没出界、不出墙壁、不是走过的位置,则向右侧走过相邻位置后继续递归搜索。向右完成后,按照同样的方式继续向下、向左、向上试探,如果这些相邻位置最终都不可行,则当前位置也不可行,于是将当前路径从路径中删除,并且顺着来的方向退回到前一位置。
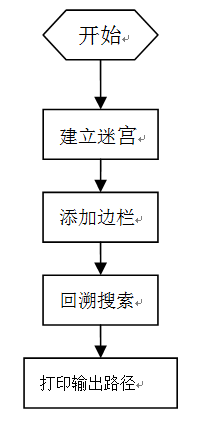
1.迷宫的描述
迷宫中存在通路和障碍,为了方便迷宫的创建,可用0表示通路,用1表示障碍,这样迷宫就可以用0、1矩阵来描述。
2.迷宫的存储:
迷宫是一个矩形区域,可以使用二维数组表示迷宫,这样迷宫的每一个位置都可以用其行列号来唯一指定,但是二维数组不能动态定义其大小,我们可以考虑先定义一个较大的二维数组maze[M+2][N+2],然后用它的前m行n列来存放元素,即可得到一个m×n的二维数组,这样(0,0)表示迷宫入口位置,(m-1,n-1)表示迷宫出口位置。