枚举法的应用举例
案例11:有不同价值、同数量的物品n件。请给出这些物品中选取一部分物品的选择方案,使选中物品的总重量不超过指定的限制重量LIMIT,但选中物品的价值之和最大。
问题分析:对于这n件物品的每一件,要么选取要么不取,因此称为0-1背包问题。考虑一个n 元组(X1 、X2,…… Xn),其中每个元素可取0或1,Xi=0表示第i个物品没有选取,而Xi=1则表示第i个物品被 选取,显然每个n元组的取值等价于一个选择方案。假设n件物品的重量和价值分别存储于数组W[ ]和V[ ]中,而n元组存放于数组X[ ]中,我们只要枚举所有的n元组,找到使得
W[1] X X[1] +W[2] X X[2] +…… +W[n] X X[n]<=LIMIT
且
V[1] X X[1] +V[2] X X[2] +…… +V[n] X X[n]的值最大
的n元组,就可以得到问题的解。
显然,每个分量取值为0或1的n元组的个数共为2n个,而每个n元组其实对应了一个长度为n的二进制数,且这些二进制数的取值范围为0~2n-1.因此,如果把0~2n-1分别转化为相应的二进制数,则可以得到所需要的2n个n元组。
案例12: 如果有3个城市A,B和C,互相之间都有往返的飞机,而且起始城市是任意的,则有6种访问每个城市的次序:ABC,ACB,,BAC,BCA,CAB,CBA。如果有4个城市,则有24种次序,可以用阶乘来表示:4!=4×3!=4×3×2×1=24;
若有5个城市,则有5!=5×4!=120,类似的有6!=720等等。即使用计算机来计算,这种急剧增长的可能性的数目也远远超过计算资源的处理能力,
Cook评论:“如果有100个城市,需要求出100!条路线的费用,没有哪一台计算机能够胜任这一任务。打个比方,让太阳系中所有的电子以它旋转的频率来计算,就算太阳烧尽了也算不完。
问题的关键是某些东西在实践中行不通。
递归法
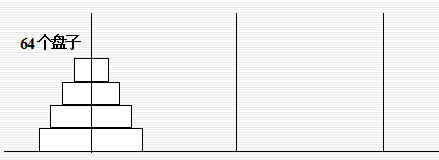
案例13:梵天塔问题 相传印度教的天神梵天在创造地球这一世界时,建了一座神庙,神庙里竖有三根宝石柱子,柱子由一个铜座支撑。梵天将64个直径大小不一的金盘子,按照从大到小的顺序依次套放在第一根柱子上,形成一座金塔如下图,即所谓的梵天塔(又称汉诺塔)。天神让庙里的僧侣们将第一根柱子上的64个盘子借助第二根柱子全部移到第三根柱子上,即将整个塔迁移,同时定下3条规则:
每次只能移动一个盘子;
盘子只能在三根柱子上来回移动,不能放在他处;
在移动过程中,三根柱子上的盘子必须始终保持大盘在下,小盘在上。
A座 B座 C座
问题分析:这个问题在盘子比较多的情况下,很难直接写出移动的步骤,可以先分析盘子比较少的情况。
假定盘子从大到小依次为:盘1,盘2,……如果只有一个盘子,则不需要利用B座,直接将盘子移动到C,如果有两个盘子,可以先将盘2 移动到B,将盘1移动到C;再将盘子2移动到C,这说明了:可以借助于将两个盘子移动到C,当然,也可以借助于C将两个盘子移动到B,如果有三个盘子,那么根据两个盘子的结论,可以借助C将盘2和盘3 从A移动到B,将盘1从A移动到C,A变成空座,将B上的两个盘子移动到C,这说明:可以借助于一个空座将三个盘子从一个座移动到另一个座。
若有三个盘子,则调用函数方式为Hanio(3,A,B,C),函数执行的过称如下图:
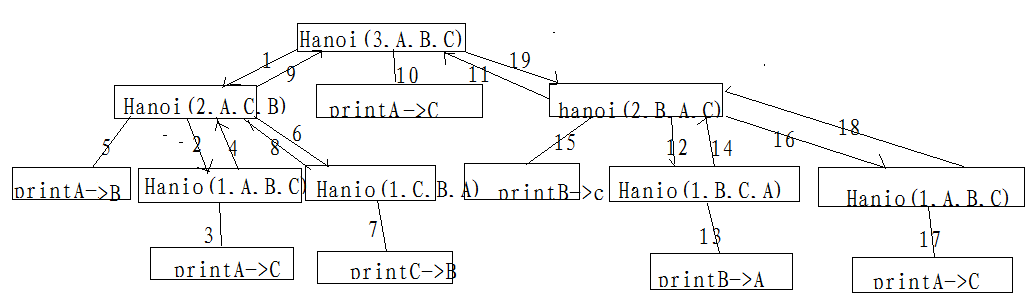
上述思想可以一直扩展到64个盘子的情况:可以借助空座C将盘子1上的63个盘子从A到B;将盘1移动到C,A就变成空座,借助于空座A,将B座上的63的盘子移动到C。
案例14:兔子繁殖问题
一般而言,兔子在出生两个月后,就有繁殖能力,一对兔子每个月能生出一对小兔子来。如果所有兔都不死,那么一年以后可以繁殖多少对兔子?
不妨拿新出生的一对小兔子分析一下:
(1)第一个月小兔子没有繁殖能力,所以还是一对
(2)两个月后,生下一对小兔民数共有两对
(3)三个月以后,老兔子又生下一对,因为小兔子还没有繁殖能力,所以一共是三对

案例15: 斐波那契数列
斐波那契数列又因数学家列昂纳多·斐波那契以兔子繁殖为例子而引入,故又称为“兔子数列”。
斐波那契数列:1、1、2、3、5、8、13、21、……
递归
如果设F(n)为该数列的第n项(n∈N+)。则:
F(1) = 1
F(2)=1
F(n)=F(n-1)+F(n-2) (n≥3)
案例16:设有一个n*m的棋盘(2≤n≤17,2≤m≤17),如下图,在棋盘上左下角有一个中国象棋马。
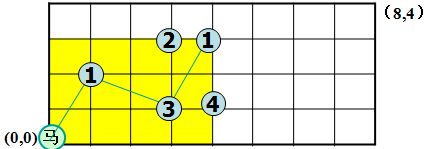
马走的规则为:①马走日字;②马只能向右走;即如下图如示:
: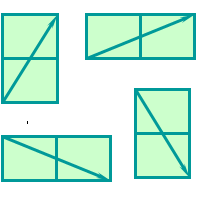
问题:当n,m输入之后,找出一条从左下角到右上角的路径。
若不存在路径,则输出“NO”.
样例
输入:4 3
输出: 0,0 -> 1,2 -> 3,1 ->4,3
递归思想就是将大问题看成规模不同大小的同样的问题。

分治策略
案例17 : 棋盘覆盖问题 问题描述:在一个2k×2k个方格组成的棋盘中,若恰有一个方格与其他方格不同,则称该方格为一个特殊方格,且称该棋盘为一特殊棋盘。显然特殊方格在棋盘上出现的位置有4k种情形。因而对任何k≥0,有4k种不同的特殊棋盘。用L型骨牌覆盖一个给定的特殊棋盘上出特殊方格外的所有方格,且任何2个L型骨牌不得重叠覆盖。
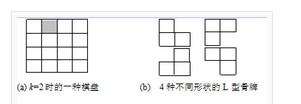
【想法】如何应用分治法求解棋盘覆盖问题呢?分治的技巧在于如何划分棋盘,使划分后的子棋盘的大小相同,并且每个子棋盘均包含一个特殊方格,从而将原问题分解为规模较小的棋盘覆盖问题。k>0时,可将2k×2k的棋盘划分为4个2k-1×2k-1的子棋盘,如图上图所示。这样划分后,由于原棋盘只有一个特殊方格,所以,这4个子棋盘中只有一个子棋盘包含该特殊方格,其余3个子棋盘中没有特殊方格。为了将这3个没有特殊方格的子棋盘转化为特殊棋盘,以便采用递归方法求解,可以用一个L型骨牌覆盖这3个较小棋盘的会合处,如图所示,从而将原问题转化为4个较小规模的棋盘覆盖问题。递归地使用这种划分策略,直至将棋盘分割为1×1的子棋盘。
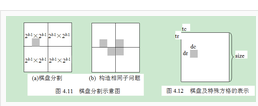
棋盘覆盖问题的方法整理如下:
(1)将整个棋盘分成四块,每块行和列都是2k-1
(2)判断每一个小的棋盘,若特殊棋子在这个区域中,则按相同的方法递归处理这个最小的棋盘,
(3)若这个棋盘中不存在特殊棋子,则根据该小棋盘的位置分别进行处理,将其转化为最小棋盘。处理方法有如下四种情况:
1.若该小棋盘在原来棋盘的左上,则在其右下方设置一个特殊字符。
2.若该小棋盘在原来棋盘的右上,则在其右下方设置一个特殊字符。
3.若该小棋盘在原来棋盘的左下上,则在其右下方设置一个特殊字符。
4.若该小棋盘在原来棋盘的右下,则在其右下方设置一个特殊字符。
经过上述的处理,各个子问题转化为与原味提相同的规模更小的问题。