变量和数组
案例6:在程序中要处理大量的类似的可变化数据,如一个班的语文成绩、一个单位的雇员姓名等,你觉得每个数据设置一个变量合适吗?如果你是高级语言的编程者,你会采用什么方法 解决问题?

在各种编程语言中,都有数据类型的变量。数组是一系列同类型且同名的变量,每个数据元素由数据名后跟”[下标]“表示。例如a[0]指示数组a中的第0个元素,a[i] 表示数组a中的第i个元素。
数组可以是一维的、二维的、三维的等。
算法的评价
案例7:有衡量时间消耗的方法,当然就有衡量空间消耗的方法,你认为能否用程序占用硬盘空间的多少作为算法的衡量的衡量空间消耗的方法吗?
从前,有一个酷爱数学的年轻国王艾述向邻国一位聪明美丽的公主秋碧贞楠求婚。公主出了这样一道题:求出48 770 428 433 377 171的一个真因子。若国王能在一天之内求出答案,公主便接受他的求婚。
国王回去后立即开始逐个数地进行计算,他从早到晚,共算了三万多个数,最终还是没有结果。国王向公主求情,公主将答案相告:223 092 827是它的一个真因子。国王很快就验证了这个数确能除尽48 770 428 433 377 171。公主说:“我再给你一次机会,如果还求不出,将来你只好做我的证婚人了。”
国王立即回国,并向时任宰相的大数学家孔唤石求教,大数学家在仔细地思考后认为这个数为17位,则最小的一个真因子不会超过9位,他给国王出了一个主意:按自然数的顺序给全国的老百姓每人编一个号发下去,等公主给出数目后,立即将它们通报全国,让每个老百姓用自己的编号去除这个数,除尽了立即上报,赏金万两。
国王最先使用的是一种顺序算法,其复杂性表现在时间方面。
后面由宰相提出的是一种并行算法,其复杂性表现在空间方面。
直觉上,我们认为顺序算法解决不了的问题完全可以用并行算法来解决,甚至会想,并行计算机系统求解问题的速度将随着处理器数目的不断增加而不断提高,从而解决难解性问题,其实这是一种误解。
阿达尔定律:设f为求解某个问题的计算存在的必须串行执行的操作占整个计算的百分比,p为处理器的数目,Sp为并行计算机系统最大的加速能力,则
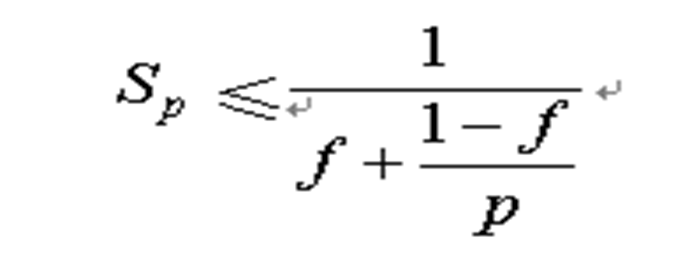
设f=1%,p→无穷大值,则Sp=100。
串行执行操作仅占全部操作1%,解题速度最多也只能提高一百倍。
对难解性问题而言,提高计算机系统的速度是远远不够的,而降低算法复杂度的数量级才是最关键的问题。
顺序查找
案例8 :某学校2004级计算机专业学生某学期成绩表,在该学期综合测评中要查找学生的各种相关信息,如查找程序设计课程最高分(98分)的学生,或查找总分最低(295分)学生;有些条件还可以同时使用,如查找数据结构和大学英语都在前三名的学生是否存在等问题,都是具有代表性的查找问题。
这是一个典型的查找问题,可将序列表A用数组表示,用数值X和系列A中的每个元素进行比较,若相等,则表示X在序列表A中存在,则查找成功,否则失败。

顺序查找实际上以关键字与序列中每个元素依次比较而确定结果的查找方法,其算法复杂度与序列表的长度有直接关系,若查找成功,则比较次数小于或者等于n,若查找不成功,则查找的次数永远为n 。查找算法的时间复杂度,其为O(n)。
折半查找
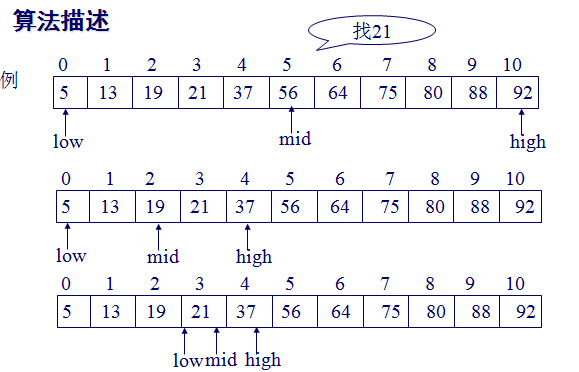
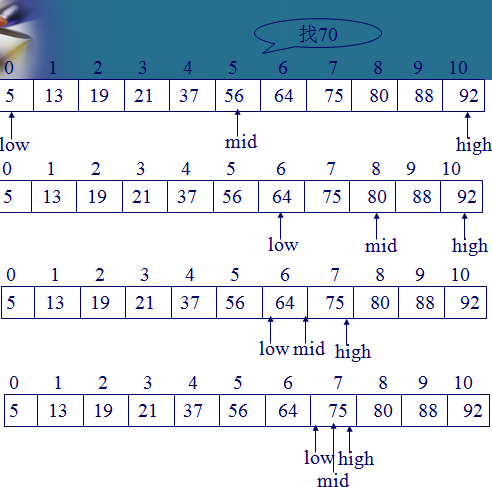
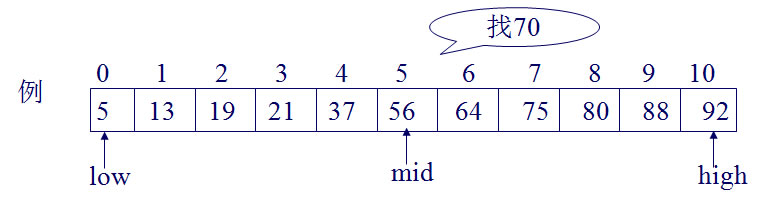
案例9: 查找过程:每次将待查记录所在区间缩小一半
适用条件:采用顺序存储结构的有序表
算法实现
设表长为n,low、high和mid分别指向待查元素所在区间的上界、下界和中点,k为给定值
初始时,令low=0,high=n-1,mid=(low+high)/2
让k与mid指向的记录比较
若k==r[mid].key,查找成功
若k<r[mid].key,则high=mid-1
若k>r[mid].key,则low=mid+1
重复上述操作,直至low>high时,查找失败
哈希查找法
案例10: 理解哈希查找的定义及其提高查找效率的思想,掌握简单哈希函数的构造方法以及冲突解决方法。
对于关键字序列A={1,5,9,13,17,……,81},建立哈希函数,并实现y=41和y=63时,哈希查找过程。
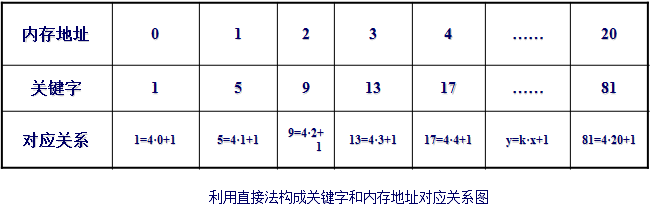
在上述对应关系中,对y=41和63进行查找,其过程如下:
(1)对于y=41,将其带入公式y=4·x+1,可得41=4·x+1,则x=10,
结论:数值为41的元素在地址为10的位置。
(2)对于y=63,将其带入公式y=4·x+1,可得63=4·x+1,则x=15.5,非整数。
结论:数值为63的元素不在该序列中。
通过直接法可在关键字和内存地址之间建立关系,利用对应关系,一次就可得到查找结果是成功还是失败。
直接法对建立对应关系的关键字要求比较高,因此,可用直接法的关键字序列比较少。