案例26:囚徒困境: 1950年,由就职于兰德公司的梅里尔·弗勒德(Merrill Flood)和梅尔文·德雷希尔(Melvin Dresher)拟定出相关困境的理论,后来由顾问艾伯特·塔克(Albert Tucker)以囚徒方式阐述,并命名为“囚徒困境”。
经典的囚徒困境如下:
警方逮捕甲、乙两名嫌疑犯,但没有足够证据指控二人有罪。于是警方分开囚禁嫌疑犯,分别和二人见面,并向双方提供以下相同的选择:
若一人认罪并作证检控对方(相关术语称“背叛”对方),而对方保持沉默,此人将即时获释,沉默者将判监10年。
若二人都保持沉默(相关术语称互相“合作”),则二人同样判监半年。
若二人都互相检举(互相“背叛”),则二人同样判监2年。

假设如同博弈论的其他例证,囚徒困境假定每个参与者(即“囚徒”)都是利己的,即都寻求最大自身利益,而不关心另一参与者的利益。
严格劣势
参与者某一策略所得利益,如果在任何情况下都比其他策略要低的话,此策略称为“严格劣势”,理性的参与者绝不会选择。
另外,没有任何其他力量干预个人决策,参与者可完全按照自己意愿选择策略。
囚徒到底应该选择哪一项策略,才能将自己个人的刑期缩至最短?两名囚徒由于隔绝监禁,并不知道对方选择;而即使他们能交谈,还是未必能够尽信对方不会反口。就个人的理性选择而言,检举背叛对方所得刑期,总比沉默要来得低。试设想困境中两名理性囚徒会如何作出选择:
若对方沉默、我背叛会让我获释,所以会选择背叛。
若对方背叛指控我,我也要指控对方才能得到较低的刑期,所以也是会选择背叛
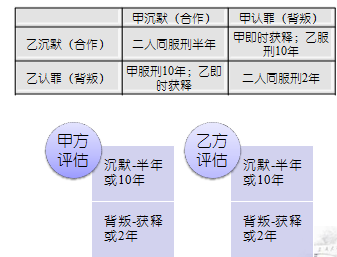
孤立地看,这是最符合个体利益的“理性”选择。
以甲为例:若乙招供,甲自己招供获刑5年,不招供获刑10年;若乙不招供,自己招供可以免刑,不招供获刑1年。
两种情况下,选择招供都更有利,事实上却比两人都拒不招供的结果糟。
由囚徒困境可知,公共生活中,如果每个人都从眼前利益、个人利益出发,结果会对整体的利益(间接对个人的利益)造成伤害。
为解决“囚徒困境”难题,美国曾组织竞赛,要求参赛者根据“重复囚徒困境”(双方不止一次相遇,“背叛”可能在以后遭到报复)来设计程序。
将程序输入计算机反复互相博弈,以最终得分评估优劣(双方合作各得3分;双方背叛各得1分;一方合作一方背叛,合作方得0分,背叛方得5分);
有些程序采用“随机”对策;
有些采用“永远背叛”对策;
有些采用“永远合作”对策;
结果,加拿大多伦多大学的阿纳托尔·拉帕波特教授的“一报还一报”策略夺得了最高分。
如果你选择“永远背叛”策略,你或许会在第一局拿到最高分,但之后的各局可能都只能拿到低分,最后虽然可能“战胜”不少对手,但由于总分很低,最终难逃被淘汰出局的命运。所以除非很难与对方再次相遇,不用担心其日后的反应,才可选择对抗与背叛;
而在长期互动、博弈的关系中,“一报还一报”是最佳策略:它是善意的,从不首先背叛;它不迂腐,不管过去相处多好,仍然对背叛有反应;它是宽容的,不因一次背叛而选择玉石俱焚。
案例27: 《论语·宪问》中,有人问孔子:“以德报怨,何如?”孔子反问:“何以报德?以直报怨,以德报德。”

”一报“还”一报“策略:
1)我方在第一次相遇时选择“合作”,之后就采取对方上一次的选择。这意味着:
2)在对方每一次背叛后,我方就“以牙还牙”,也背叛一次;
3)对方每一次合作后,我方就“以德报德”一次;
该策略有别于“善良”的“永远合作”或“邪恶”的“永远背叛”对策,及对方一旦“不忠”,我方就不再给机会,长久对抗的策略。