案例11:猜数。请默默选中一个数,告诉我哪些卡片上有这个数
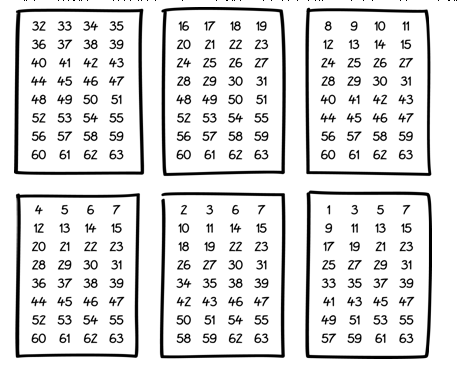
案例12:类似游戏:猜姓

引出的知识:
1、二进制和十进制
2、信息编码的基本概念
拓展思考:
1、对应三进制的表怎么构造
2、是否可以构造不等大小的表
3、是否可以构造一个同时猜姓和属相的游戏
案例13 :猜属相,猜你所说出的属相在那个方格里?

案例14:小明是个卖苹果的,小红一次在小明那买N(N<1024)个苹果。小明每次都要数N个苹果给小红,唉,太麻烦了。于是小明想出了一种方法:他把苹果分在10个袋子中,则无论小红来买多少个苹果,则他都可以整袋整袋的拿给小红。问怎样分配苹果到各个袋子?
此问题用二进制编码思想可以轻松解决。
按照二进制编码的特点,n位二进制数的各个数位的权重从低到高分别是2^0 ,2^1 , 2^2 ,…… 2^( n– 1 )。n位无符号二进制数可以表示0到(2^n)- 1 ,共n个数。
而二进制数位只有1和0两种状态,正好对应题目中苹果袋子的“给”与“不给”两种状态。因此只要将各个袋子分别装入 2^0 , 2^1 , 2^2 ,……, 2^9 个苹果即可满足题目要求。例如:需要66个苹果,因66的二进制是 1000010 ,则小明只要将苹果个数为2^1(2个)和2^6(64个)的袋子给小红就可以了。
不同数值之间的转换
案例15:十进制转换成二进制
通过五张数字游戏,已经知道如何写出与0~31之间的十进制数等值的5位二进制数表示。现在给定任意一个十进制数(不限于0~31),利用类似的思想写出与之等值的二进制数。
数字6如何表示?
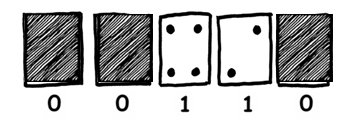
利用上述的思想,如8=1000,9=1001,10=1010.

从二进制的权表达式还能看出二进制的几个性质:
(1)第i项的权值是第i-1项的权值的两倍
(2)第i项的权值等于其后所有项的权值之和再加1
(3)整数部分右边插入一个0(相当于整数部分左移1位)等价于整数部分乘2,小数部分左边插入一个0(相当于小数部分右移1位)等价于小数部分除2
(4)小数点右移一位相当于乘2,小数点左移一位相当于除2
十进制的BCD码
案例16:至少需要使用多少位二进制编码来表示十进制的0~9这10个符号?
十进制数的0~9共10个符号,所以至少使用4位二进制编码来表示,因为4位二进制编码有16种组合,BCD码至少需要使用其中的10种组合,剩下的六种不用,实际上常用的BCD编码方案只有很少的几种。

思考:(1)在计算机中,字符“0”~“9”和数字0~9的二进制编码编码表示是一样的吗?
(2)数25的二进制编码和8421码表示是一样的吗?什么情况下一个数的二进制编码和8421码表示是一样的,什么情况下不一样的?
二进制的运算
案例17:二进制的加、减、乘、除运算规则如下:
加法:0+0=0,0+1=1,1+0=1;1+1=0(有进位)
减法:0-0=0,0-1=1(有借位),1-0=1;1-1=0
乘法:0X0=0,0X1=0,1X0=0,1X1=1
除法:0/1=0,1/1=1
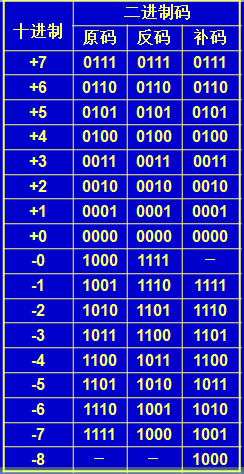
若n位二进制数的原码为N,则反码为:[N]反=(2n –1)- N,(0变1,1变0)即得反码 把原码各位求反
补码:若n位二进制数的原码为N,则补码为:N]补=2n – N=[N]反+1,把原码的各位求反后加1即得补码。
[5]原=0101 [5]反=1010 [5]补=1011
带符号的二进制数用最高位表示符号,称为符号位,且0表示正,1表示负,其余位表示绝对值的值,称为数值位。表示


n位带符号二进制数码可以表示的数值范围:
原码: -(2n-1-1) ~+(2n-1-1)
反码: -(2n-1-1) ~+(2n-1-1)
补码: -2n-1 ~+(2n-1-1)
图像信息的表示
案例18:记录每个白色或黑色连续区域的长度。
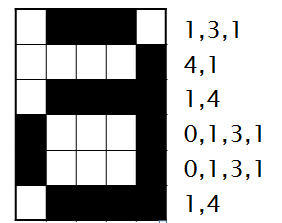
灰度图像常用2~10个比特来描述一个像素的灰度级别。如果说单色图像如同剪纸的逼真 ,那么灰度图像则与黑白照片效果相似,灰度级越多,图像看起来越逼真。
布尔运算
案例19:计算机显示器显示的如何颜色都可以用三种基本色(即三原色):红绿蓝混合组成。例如:红+绿=黄、绿+蓝=青等等。试想一种简单的情况,使用三种不同颜色的光源投射到玻璃屏幕上,每种光源都能打开或关闭。那么基于光源的R(红)、G(绿)、B(蓝)的关闭(0)或打开(1),屏幕上就会看到8种不同的颜色:
| R G B | 颜色 | R G B | 颜色 |
| 0 0 0 | 黑 | 1 0 0 | 红 |
| 0 0 1 | 蓝 | 1 0 1 | 红紫 |
| 0 1 0 | 绿 | 1 1 0 | 黄 |
| 0 1 1 | 蓝绿 | 1 1 1 | 白 |
这些元组的集合组成了一个八元素布尔代数。
(1)一些颜色的补是通过关闭那些打开的颜色光源,且打开那些关闭的颜色光源而形成的。上面列出的八种颜色的补是什么?
(2)对于这种代数,布尔值0和1对应的颜色是什么?
(3)描述下面的颜色用布尔运算结果:
蓝色|红色=?
红紫色&黄绿色=?
绿色^红色=?
在文献搜索时使用了布尔运算的概念。对于一个用户输入的关键词,搜索引擎要判断每篇文章是否含有这个关键词,如果一篇文章含有这个关键词,就相应地给这个关键词一个逻辑真值,否则,给一个逻辑假值。例如要查找有关原子能应运的文献,但并不想知道如何制造原子弹,则可以这样写查询条件”原子能AND应用AND(NOT原子弹)“,表示符合要求的文献必须满足三个条件:(1)包含原子能 (2)包含应用 (3)不包含原子弹
一篇文献对于上面每一个条件,都有一个true或false的结果,再将所有结果进行”与“运算就能计算出每篇文献是否满足要求。
存储器存储信息
案例20:要到某个住宅小区去找你朋友,你需要知道什么信息才能找到他?
计算机存储单元是在是太多,为了区分个存储单元,计算机科学家为每一个为了区分各存储单元都编了号,这些编号就称为地址。地址从0 开始编排,一直到最大的地址编号2n-1(n是地址的位数)。这样的编址方法不仅提供了唯一标识每个存储单元的方法,而且也给存储单元赋予顺序的概念,这样就有了”当前单元“、”下一个单元“、”前一个单元“的说法。
案例21: 存储器存取信息和仓库这两件事情,抽象后可以认为都是存取某种对象。那么二者之间的区别?
由于信息的可复制性,所以将存储器理解为存储信息的仓库是不准确的。信息的写入和读出这两种操作完全不同于仓库的货物的入库和出库。对存储器进行读操作时,读出的是所保存信息的拷贝,原来的信息仍然存在,对存储器进行读操作时,读出的是所保存信息的拷贝,原来的信息仍然存在;对存储器的写入操作则是覆盖性的写入 ,原来的信息会被新的信息所代替。