信息
案例1:请从信息量的高低排列以下书籍
(1)500页的电话簿
(2)1000页空白纸
(3)1000页写满“废话 废话 废话”的纸
(4)1000页的电话簿
思考:一本1000页的书有多少信息呢?
案例2:在那天人们知道美国纽约世贸大厦被炸和 在今天人们知道美国纽约世贸大厦被炸的信息量那个大?

案例3:回答以下问题:
(1) 通过截屏截取同样大小的两张照片,一张空白,另一张有内容,这两张图片的像素是相等的,但那张图片包含的信息多?
(2)你要到电影院去找一个人。甲告诉你两条消息:1、他不坐在前10排 2、他也不坐在后10排;而乙只告诉你一条消息:他坐在第15排。问甲和乙谁提供的信息量大?
(3)在盛夏季节,气象台突然预报“明天无雪”,这条信息包含的信息量是多少?
在事件发生前有不确定度、在事件发生时有惊讶度、在事件发生后有信息量,当一个概率很低的随机事件发生,我们就会感到非常惊讶,并得到很大的信息量。
一条信息的信息量大小和它所消除的不确定有直接的关系。例如:要搞清楚一件非常不确定的事,或者一无所知的事情,就需要大量的信息。相反,如果对某件事情已经有了较多的理解,则不需要太多的信息就能把它搞清楚。所以,从这个意义上说,可以认为信息量的大小就等于它所消除的不确定性的程度。
对概率有所了解的人都知道,不确定性是与“多种结果的可能性”相联系的。而在数学上,这种可能性正是以概率来度量的。在日常生活中,极少发生的事件一旦发生是容易引起人们的关注的,而司空见惯的事不会引起注意,这意味着罕见事件所带来的信息量比较多。如果用统计学的术语来描述,这就出现概率小的事件的信息量大。例如:海啸带来的信息量要比下雨事件带来的信息量大的多。因为海啸很少见,容易形成新闻热点,而下雨是司空见惯的。
由于小概率事件的发生比大概率事件的发生更使人感到惊讶,所以计算机科学家常用一段消息的“惊奇度”来衡量该消息中所含有的信息量。例如:你的朋友问你你今天是怎么来学校的,而他正好是走路来上学的,你很可能就第一次就猜中。如果要猜中乘私家车来的话,大概需要多猜几次,如果是乘坐直升飞机的话,大概会更难猜。由此可知,“走路来上学”、“乘私家车”、“乘坐直升飞机”这三条信息所包含的信息量是依次增大的,也就是说你猜测的次数会依次增加。
案例4:(1)将学生分成每两人一组。每组中一个人任意想一个1~100之间的数字,另一个来猜,猜的人可以问任意问题,前者只能回答yes/no。试用最少的次数猜出答案,估计用几次才能猜到正确答案?
(2)如果要猜的数是你搭档的年龄,换需要才那么多次吗?如果猜的数在1~10000之间,猜的次数要增加100倍吗?
在猜测中只能回答yes/no,因此也可以用二进制1和0来取代这两种提示答案,从而可以将比特或二进制位作为计算信息量的单位。下表是锁定某一数值范围之间的任意一个数字所包含的信息量。
表2-1
| 数值范围(十进制) | 信息量(比特) | 数值范围(十进制) | 信息量(比特) |
| 1~10 | 4 | 1~10000 | 14 |
| 1~100 | 7 | 1~1000000 | 17 |
| 1~1000 | 10 |
上表示如何构造出来的啊?如何将该表扩展到任意数值范围?如果你能找到使猜测最少的办法,实际就找到了问题的答案了。图2-1是一个解决猜测0~7之间任意一个数的决策树,猜测方法是从树的顶部开始提问,然后根据得到的答案沿着树枝的走向提出下一个问题,直到得到答案。
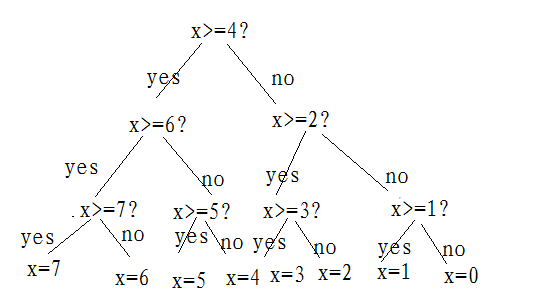
图2-1
案例5:(1)如果目标数字为5,yes/no的序列应该是什么?该序列包含几个回答?回答的个数和目标值有什么 关 系?
(2)如果将决策树中的yes用1表示,no用0表示,0~7均用二进制数来表示。回答以上的问题。
可以看出,决策树的最底层的二进制数字就是问题的一系列yes/no回答。如果每个数字出现的概率相同的话,那么得到目标数字所需长长的次数,就等于二进制表示该数字所采用的位数。
好的策略:(1) 每次提问将消息范围缩小一半。
(2)如果范围从0-100扩大到0-1000,不用多花10倍的努力来找到答案——只需要比原来多问三个问题即可。
(3)每当范围加倍时只需要多提一个问题即可找到答案。
猜想:(1)在一个范围内,比如[1, 1,000,000],秘密地选定一个数字
(2)每一次观众都可以问一个问题,而回答只能是“yes” 或者“no”。重复进行,最终,观众往往能得到基于x的正确答案。
(3)为了找出x,观众需要提问多少次
案例6:Shannon对使用自然语言(如英语)表达的消息所含信息量的多少这个问题十分入迷,他做了一个实验,让人们通过逐个猜字母的方式来猜句子。向实验者展示部分文本,让他猜下一个字母,如果猜错了,告诉他并让其再猜,直到正确。:如Shannon实验中的文本“there is no reverse on a motorcycle. a friend of mine found this out rather dramatically the other day.”(为了容易猜,他省略了标点和大写),一个典型的实验结果如下:

案例7:甲乙两人玩掷棋子游戏,甲准备在8*8的方格上随意放一个棋子,在乙看来所放的位置是不确定的。
(1)在乙看来棋子放在某方格的不确定性为多少?
(2)若甲告知乙所放位置的行号。这时在乙看来棋子放在某方格的不确定性为多少?
(3)若甲将棋子所放方格的行号和列号都告诉乙,在乙看来棋子在某方格的不确定性为多少?
有多种关于信息的定义,从其关注的角度大体可分为3类:
1)信息论角度
消息中所含有的对接受者而言的“未知性”或“不确定性”则称为信息。
2)哲学角度(钟义信教授)
本体论层次——事物的运动状态及其变化方式的自我表述。
认识论层次——认知主体所表述的关于该事物的运动状态及其变化方式,包括这种状态/方式的形式、含义和效用。
3)知识管理角度-DIKW(Data, Information, Knowledge, Wisdom) 体系信息是经过加工处理的、具有一定含义的,存在逻辑关联的、有时效性的、对决策有价值的数据。 它回答了“who”, “what”, “where”, and “when” 等问题。
案例8 :我们以一届世界杯决赛的冠军队的信息为认知对象来举例说明。
认知者:没有看比赛的某个人来猜测冠军
边界:已知32个球队的队名,按0~31顺序编号
随机性:有热门队,也有黑马队,尽管夺冠可能性不同,但结果出来之前一切皆有可能。
判决: “猜不中A”的机会与“A夺冠的可能性”成反比。若32支队伍的实力相当,每个队夺冠的概率均为pi=1/32。
每次猜测的过程为:把当前对象分为下半区和上半区两个部分,分别以二进制数“0”、“1”标记,猜冠军在哪一个区。每猜一次都只有对或错两种可能,由已知结果的人作为裁判(判决器),错误用“F”标识、正确用“T”标识,每次判决获得1位二进制数信息。猜测结束后可以由各次猜测的结果精确地确定冠军队编号。“猜中”所需的猜测次数越多,“猜中”得到的信息量就越大。
保证“猜中”所需的猜测次数可以推算如下:

总共判断了5次,结果清楚地标识出具体的队号。
参赛队越多,“猜中”需要的次数也就越多,结果需要用更多位数表示。
队数多了,每个队夺冠的概率就变小,而“猜中”的信息量就变大。若只有一个参赛队,不用猜也能知道结果,故猜中的信息量为0。
每猜一次,获得一位信息,“不确定性”就会减少一半,=>香农在其《通信的数学理论》一文中把信息量定义为随机不确定性减少的程度。
数的二进制表示
案例9: 有16种溶液,其中有且只有一种是有毒的,这种有毒的溶液与另一种试剂A混合会变色,而其他无毒溶液与A混合不会变色。已知一次实验需要1小时,由于一次混合反应需要使用1个试管,问最少使用多少个试管可以在1小时内识别出有毒溶液?
如果没有1小时的时间限制,那么利用二分搜索的思想既可以解决问题。(第一次取16种溶液中的8种放入一个试管,然后加入试剂A,看有没有反应,根据结果再进行细分。这样只需4个试管,但是需要4个小时)有了这个1小时的时间限制后这种方法就不管用了。一种正确的解答如下:
首先,将16种溶液编号为0到15编号的二进制形式表示:0001、0010、0011、0100、0101、0110、0111、1000、1001、1010、1011、1100、1101、1110、1111。
然后,取4个试管,第一个试管加入编号二进制形式中第一位(指最低位)是1的溶液,第二个试管加入编号第二位是1的溶液,其他2个试管分别加入编号第3,4位为1 的溶液。然后再将试剂A加入4个试管中,看那些试管发生了反应,就可以知道有毒溶液的编号了。例如:第1、2、4号试管内发生了反应,则我们知道是第7号溶液是有毒的。原因是7的二进制编码是1011,因此7号溶液是唯一加入了1、2、4号试管,而没有加入3号试管的溶液。
案例10:准备5张卡片,反面空白,正面有不同的点数,样子和排列顺序如下图所示。请用它们表示0~31中任意一个数,如25(注意卡片顺序不要改变,只翻转正反面)。
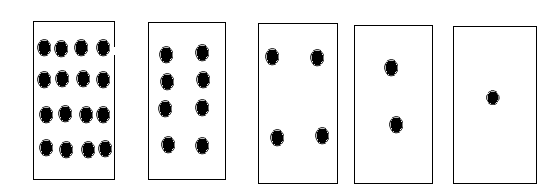
具有不同点数的卡片数
如果将反面反面朝2上的记做0,正面朝上的记做1,例如15用"正/反“表示为”反正正正正正“, 而用0/1序列表示为”011111“。
在以上的练习的基础上,回答以下问题。
(1)在上述序列的左面再增加若干张卡片,它们的点数应该是多少?规律是什么?
(2)5张卡片能表示的最大数和最小数是多少?写出对应的0/1序列表示。
(3)5张卡片的点数分别是2的多少次方?如果从右向左给卡片编号为0~4,那么卡片编号与卡片的方次数之间的关系是什么?