4 .3 数据库系统的基本概念 　　

　　关系数据库系统的特点之一是它建立在数学理论的基础之上，有很多数学理论可以表示关系模型的数据操作，其中最著名的是关系代数（ relational algebra ）与关系演算（ relational calculus ） . 数学上已经证明两者在功能上是等价的。下面将介绍关于关系数据库的理论——关系代数。

　  1.关系模型的基本操作
　  关系是由若干不同的元组所组成，因此关系可以视为元组的集合。 n 元关系是一个 n 元有序组的集合。设有一个 n 元关系 R ，它有 n 个域，分别是 D1 ， D2 ， …Dn, 此时，它们的笛卡尔积是：D1*D2* … *Dn ，该集合的每个元素都是具有如下形式的 n 元有序组：
　                                    （ d1,d2, … ,dn ） di ∈ Di(i=1,2,3,…,n)
 　 该集合与 n 元关系 R 有如下关系　　R
 　 即 n 元关系 R 是 n 元有序组的集合，是它的笛卡儿积的子集。
　  关系模型有插入、删除、修改和查询四种操作，它们又可以进一步分解成六种基本操作：
　  •  关系的属性指定。指定一个关系内在的某些属性，用它确定关系这个二维表中的列，主要用于检索或定位。
　　•  关系的元组的选择。用一个逻辑表达式给出关系中所满足此表达式的元组，用它确定关系这个二维表的行，它主要用于检索或定位。
用上述两种操作即可确定一张二维表内满足一定行、列要求的数据。
　　•  两个关系的合并。将两个关系合并成一个关系。用此操作可以不断合并从而可以将若干个关系合并成一个关系，以建立多个关系间的检索与定位。
　　用上述三个操作可以进行多个关系的定位。
　　•  关系的查询。在一个关系或多个关系间做查询，查询的结果也为关系。
　　•  关系元组的插入。在关系中添加一些元组，用它完成插入与修改。
　　•  关系元组的删除。在关系中删除一些元组，用它完成删除与修改。

　　2 ．关系模型的基本运算
　　由于操作是对关系的运算，而关系是有序组的集合，因此，可以将操作看成是集合的运算。
　　（1）插入
　　设有关系 R 需插入若干元组，要插入的元组组成关系 R ′ ，则插入可用集合并运算表示为： R ∪ R ′
　　（2）删除
　　设有关系 R 需删除一些元组，要删除的元组组成关系 R ′ ，则删除可用集合差运算表示为： R — R ′
　　（3）修改
　　修改关系 R 内的元组内容可以用下面的方法实现：
　　 •  设需修改的元组构成关系 R ′ ，则先做删除得
　　　　R — R
　　 •  设修改的元组构成关系 R″，此时将其插入即得到结果：
　　　 （R—R′）∪R″
　 （4） 查询
　　用于查询的三个操作无法用传统的集合运算表示，需要引入一些新的运算。
　   •  投影（ Projection ）运算
    对于关系内的域指定可引入新的运算叫投影运算。投影运算是一个一元关系，一个一元关系通过投影运算（并由该运算给出所指定的属性）后乃为一个一元关系 R ′ 。 R ′ 是这样一个关系，它是 R 中投影运算所指出的那些域的列所组成的关系。设 R 有 n 个域： A1 ， A2 ， …An,则在 R 上对域 Ai1,Ai2,…,Aim(Aij ∈ ｛ A1,A2,…,An ｝ ) 投影可表示成为下面的一元运算：
π Ai1,Ai2,…,Aim(R)
　　 •  选择（ selection ）运算
　　选择运算也是一个一元运算，关系 R 通过选择运算（并由该运算给出所选择的逻辑条件）后仍为一个关系。这个关系是由 R 中那些满足逻辑条件的元组组成。设关系的逻辑条件为 F ，则 R 满足 F 的选择运算可写成为：
　　б F （ R ）
　　逻辑条件 F 是一个逻辑表达式，它是由下面的规则组成。
　　它可以是具有 αθβ的形式，其中α，β是域（变量）或常量，但是α，β又不能同为常量，θ是比较符，它可以是 <,>,≤,≥,=及≠。αθβ叫基本逻辑条件。
　　由若干个基本逻辑条件经过逻辑运算得到，逻辑运算为∧、∨及∽构成，称为复合逻辑条件。
　　有了上述两个运算后，我们对一个关系内的任意行、列的数据都可以方便地找到。
　　 •  笛卡儿积（ Cartesian Product）运算
　　对于两个关系的合并操作可以用笛卡儿积表示。设有n元关系R及m元关系S，它们分别有P、 q个元组，则关系R与S经笛卡儿积记为R*S，该关系是一个n+m元关系，元组个数是p*q, 由R与S的有序组组合而成。
　　表4.4给出了两个关系R、S的实例以及R与S的笛卡儿积T=R*S。
　　　　　　　
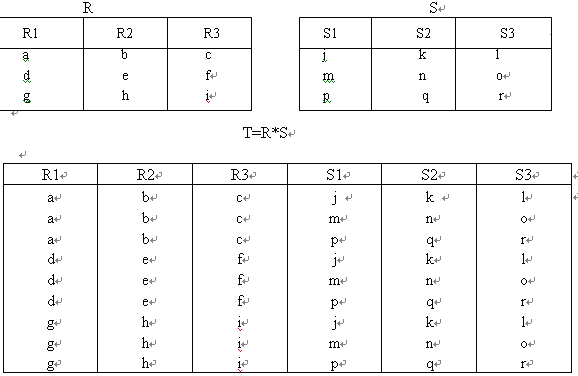
　　　　　　　　　　　　　　　　　　　　　　　表4.4　R、S的实例以及R与S的笛卡儿积T=R*S

　  3．关系代数中的扩充运算
　　关系代数中除了上述几个最基本的运算外，为操纵方便还需增加一些运算，这些运算均可由基本运算导出。常用的扩充运算有交、除、连接及自然连接等。
　　（1）交（ intersection ）运算
　　关系 R 与 S 经交运算后所得到的关系是由那些即在 R 内又在 S 内的有序组所组成，记为 R ∩ S 。
　　表 4.5 给出了两个关系 R 与 S 及它们经交运算后得到的关系 T 。
　　　　　　　
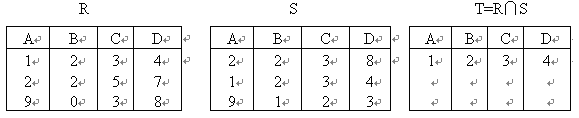
　　　　　　　　　　　　　　　　　　　　　　　　　表4.5　 关系 R 、 S 及 R ∩ S
　　交运算可由基本运算推导而得：R ∩ S=R(R-S)
　  （2） 除（ division ）运算
　   如果将迪卡尔积运算看作乘运算的话，那么除运算就是它的逆运算。当关系 T=R*S 时，则 、可将除运算写成为：
　　 T/R=S 或 T/R=S
　　 S 称为 T 除以 R 的商（ quotient ） .
　  由于除是采用的逆运算，因此除运算的执行是需要满足一定条件的。设有关系 T ， R ， T 能被除的充分必要条件是： T 中的域包含 R 中的所有属性： T 中有一些不出现在 R 中。
　  在除运算中 S 的域由 T 中那些不出现在 R 中的域所有组成，对于 S 中任一有序组，有它与关系 R 中每个有序组所构成的有序组均出现在关系 T 中。
　  表 4.6 给出了关系 R 及一组 S ，对这一组不同的 S 给出了经除法运算后的商 R/S ，从中可以清楚地看出除法的含义及商的内容
　　　　　　
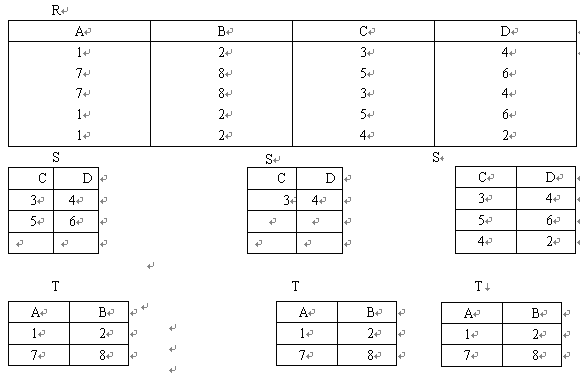
　　　　　　　　　　　　　　　　　　　　　　　　　表4.6　三个除法
　　 除法运算不是基本运算，它可以由基本运算推导出。设关系 R 有域 A1 ， A2 ，……， An ，关系 S 有域 An-s+1, An-s+2, …… ,An-s, 此时有：
　　 R ÷ S= Π A1，A2，…,An_s((ΠA1,A2,…An_s(R)*S)-R)
　　 除法的定义虽然较复杂，但在实际中，除法的意义还是比较容易理解的。
　　 例 4.2 设关系R给出了学生修读课程的情况，关系S 给出了所有课程号，分别如表4.7（a）,(b)所示。 试找出修读所有课程的学生号。
　　 解：修读所有课程的饿学生号可用 T=R/S 表示，结果如表 4.7(c) 所示
　  (3) 连接 (join) 与自然连接（ natural join ）运算
　  在数学上，可以用笛卡儿积建立两个相互连接的关系往往须满足一些条件所得到的结果也较为简单。这样就引入了连接运算与自然连接运算。
　  连接运算又可称为 θ - 连接运算，这是一种二元运算，通过它可以将两个关系合并成一个大关系。设有关系 R 、 S 以及比较式 i θ j, 其中 I 为 R 中的域， θ含义同前。则可以将 R、S在域i ,j上的θ连接记为 ：R|*|S
　　　　　　　　　　
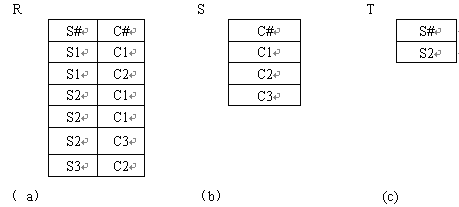
　　　　　　　　　　　　　　　　　　　　　　表4.7　学生修读课程的除法运算
　　 它的含义可以用下式定义：
　　 R|*| S= δ i θ j (R*S)
　　 即 R 与 S 的 θ 连接是由 R 与 S 的笛卡儿积中满足限制 i θ j 的元组构成的关系，一般其元组的数目远远少于 R*S 的数目。应当注意的是，在 θ 连接中， i 与 j 需具有相同域，否则无法作比较。
　　 在 θ 连接中如果 θ为“ =”，就称 此连接为等值连接，否则称为不等值连接；如 θ为“ <” 时称为小于连接；如果θ为“>”时称为大于连接。
　　 例4.3 设有关系R、S分别如表4.8(a),(b)所示，则T1=R|*|S如表 4.8（c）所示的关系，T2=R|*|S为如表 4.8（d）所示的关系。
　　　D>E D=E
　　　　　　　　
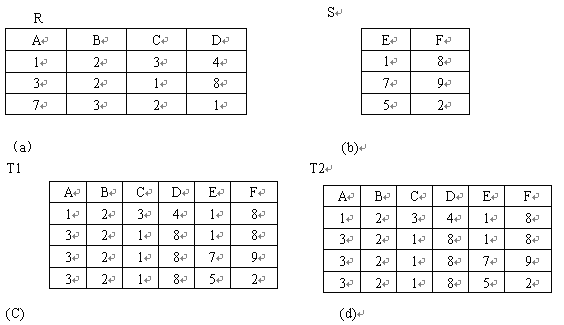
　　　　　　　　　　　　　　　　　　　　　表 4.8R 、 S 及 T1=R|*|S ， T2=R|*|S

　  在实际应运中最常用的连接是一个叫自然连接的特例。它满足下面的条件：
　  •  两关系间有公共域；
　  •  通过公共域的相等值进行连接。
　  设有关系 R 、 S ， R 有域 A1 ， A2 ，…， An,S 有域 B1,B2, …， Bm, 并且 A1 ， A2 ，…， An, 与 B1,B2, …， Bm, 分别为相同域，此时它们自然连接可记为：R|*|S
　  自然连接的含义可用下式表示：
　  R|*|S= Π A1，A2，…,An， B1,B2, …， Bm （ б Ail=Bl1Ai2=B2^…^Aij=Bj(R*S))
　  例 4.4 设关系 R ， S 如表 4.9 （ a ）（ b ）所示，则 T=R|*|S 如表 4.9 （ c ）所示。
　　　　
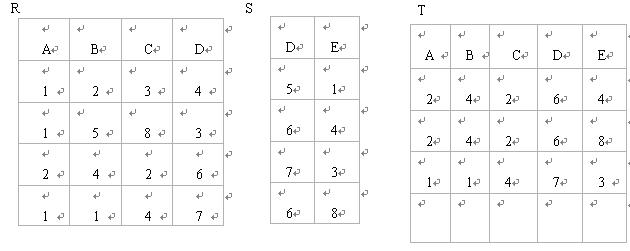
　　　　　　　　　　　　　　　　　　　　　　　　　　表4.9 　R、S及T=R|*|S
　　在以上运算中最常用的是投影运算、选择运算、自然连接运算、并运算及差运算。

　　4 ．关系代数的应用实例
　   关系代数虽然形式简单，但它已经足以表达对表的查询、插入、删除及修改等要求。在所有这些操作中，查询是最复杂的操作。在 20 世纪 70 年代，关系数据库系统始终无法走向商品化，最主要的原因是它的查询效率低下。关系数据库的查询语言一般是非过程语言，即仅仅说明要查询的要求，而不说明如何去进行查询。最终，通过查询优化技术解决了此问题，而对于查询语句（即代数表达式）本身的优化即代数优化是最基本的技术。下面通过一个例子来体会一下如何将关系代数应用于查询。
　  例 4.5 建立一个学生选课的关系数据库，它由下面三个关系模式组成：
　　 S （ S# ， Sn, Sd, Sa ） ;
　　 C (C#, Cn,P#);
　　 SC (S#, C#, G).
　  其中 S# ， C# ， Sn, Sd, Sa, Cn, P#, G 分别表示学号、课程号、学生姓名、学生系别、学生年龄、课程名、预修课程号、成绩，而 S 、 C ， SC 则分别表示学生、课程、学生选课关系。
　  写出对关系模式 S 、 C 和 SC 中的下述查询表达式：
　 （1）检索所有学生情况： S
　 （2）检索学生年龄大于等于 20 岁的学生姓名： π Sn（δSa≧20(S)）
　 （3）检索预修课程号为C2的课程的课程号： π c#（δp#=c2(C)）
　 （4）检索课程号为C，且成绩为A的所有学生姓名： π Sn（δC#C∧G=A(S|*|SC)）
　 注意：这是一个涉及到两个关系的检索，此时需用连接运算。
　 （5）检索S1所修读的所有课程名及其预修课号： π cn,p#（δS#=S1(C|*|SC)）
　 （6）检索年龄为 23 岁的学生所修读的课程名： π cn（δSa=23(S|*|SC|*|C)）
　  注意：这是涉及到三个关系的检索。
　 （7） 检索至少修读 S5所修读的一门课的学生姓名。
　  这个例子比较复杂，需作一些分析。将问题分以下三步解决：
　  第 1步：取得S5修读的课程号，它可以表示为：
　  R= π C#（δS#=S2(SC)）
　  第 2 步：取得至少修读为 S5 修读的一门课的学号：
　  W=π S#（SC|*|R）
　  第 3 步：最后结果为：
　  π Sn (S|*|W)
　  分别将 R 、 W 代入后即得所要求之表达式：
　  π Sn（S|*|( π s#(SC|*|( πc#( δ s#=s5(SC) ) )))）
　  对于一般较为复杂的查询，都是通过这样的步骤来解决的。注意到该过程中会产生一些中间的表，而查询优化中一般应尽可能使这些中间表较小。