1.6.1 树的基本概念
1.6.2 二叉树及其基本性质
1.6.3 二叉树的存储结构
1.6.4 二叉树遍历
1.6.1
树的基本概念 
树( tree )是一种简单的非线性结构。在树这种数据结构中,所有数据元素之间的关系具有明显的层次特性。图 1.26 表示了一棵一般的树。由图 1.26 可以看出,在用图形表示树这种数据结构时,很像自然界中的树,只不过是一棵倒长的树,因此,这种数据结果就用“树”来命名。
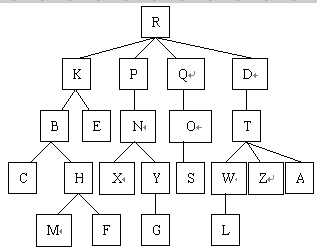
图1.26 一般的树
在树的图形表示中,总是认为在用直线连起来的两端结点中,上端结点是前件,下端结点是后件,这样,表示前后关系的箭头就可以省略。
在现实世界中,能用树这种数据结构表示的例子有很多。例如,图 1.27 中的树表示了学校行政关系结构;图 1.28 中的树反映了一本书的层次结构。由于树具有明显的层次关系,因此,具有层次关系的数据都可以用这种数据结构来描述。在所有的层次关系中,人们最熟悉的是血缘关系,按血缘关系可以很直观地理解树结构中各数据元素结点之间的关系,因此,在描述树结构时,也经常使用血缘关系中的一些术语。
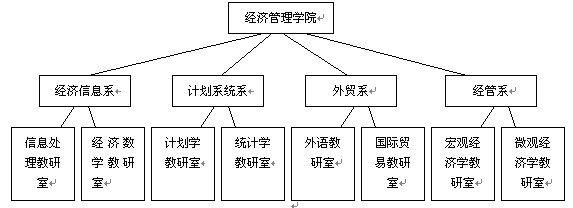
图1.27 学校行政层次结构
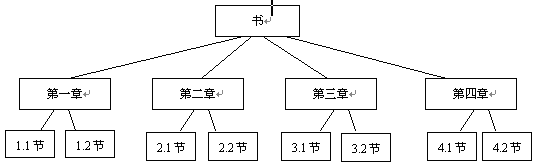
图1.28 树的层次结构
下面介绍树这种数据结构中的一些基本特征,同时介绍有关树的基本术语。
在树结构中,每一个结点只有一个前件,称为父结点,没有前件的结点只有一个,称为树的根结点,简称为树的根。例如,在图 1.26 中,结点 R 树的根结点。
在树结构中,每一个结点可以有多个后件,它们都称为该结点的子结点。没有后件的结点称为叶子结点。例如,在图 1.26 中,结点 C 、 M 、 F 、 E 、 X 、 G 、 S 、 L 、 Z 、 A 均为叶子结点。
在树结构中,一个结点所拥有的后件个数称为该结点的度。例如在图 1.26 中,根结点 R 的度为 4 ;结点 T 的度为 3 ;结点 K 、 B 、 N 、 H 的度为 2 ;结点 P 、 Q 、 D 、 O 、 Y 、 W 的度为 1 ,叶子结点的度为 0 。在树中,所有结点中最大的度称为树的度。例如,图 1.26 所示的树的度为 4 。
前面已经说过,树结构具有明显的层次关系,即树是一种层次结构。在树结构中,一般按如下原则分层:根结点在第一层。
同一层上所有结点的子结点都在下一层。例如,在图 1.26 中,根结点 R 在第 1 层;结点 K 、 P 、 Q 、 D 在第 2 层;结点 B 、 E 、 N 、 O 、 T 在第 3 层;结点 C 、 H 、 X 、 Y 、 S 、 W 、 Z 、 A 在第 4 层;结点 F 、 M 、 G 、 L 在第 5 层。
树的最大层次称为树的高度。例如,图 1.26 所示的树的高度为 5.
在树中,以某结点的一个子结点为根构成的树称为该结点的一棵子树。例如,在图 1.26 中;结点 R 有 4 棵子树,它们分别以 K 、 P 、 Q 、 D 为结点;结点 P 有 1 棵子树,其根结点为 N; 结点 T 有 3 棵子树 ; 它们分别以 W 、 Z 、 A 为结点。
在树中,叶子结点没有子树。
在计算机中,可以用树结构来表示算术表达式。
在一个算术表达式中,有运算符和运算对象。一个运算符有多个运算对象。例如,取正( + )与取负( - )运算符只有一个运算对象,称为单目运算符;加( + )、减( - )乘( * )、除( / )、乘幂( ** )运算符有两个运算对象,称为双目运算符;三元函数 f(x,y,z) 中的 f 为函数运算符,它有三个运算对象,称为三目运算符;一般来说,多元函数有多个运算对象,称为多目运算。算术表达式中的一个运算对象可以是子表达式,也可以是单变量(或单变数)。例如,在表达式 a*b+c 中,运算符“ + ”有两个运算对象,其中 a*b 为子表达式, c 为变量 ; 而在子表达式 a*b 中,运算符“ * ”有两个运算对象 a 和 b, 它们都是单变量。
用树来表示算术表达式的原则如下:
• 表达式中的每一个运算符在树中对应一个结点,称为运算符结点。
• 运算符的每一个运算对象在树中为该运算符结点的子树(在树中的顺序为从左到右)。
• 运算对象中的单变量均为叶子结点。
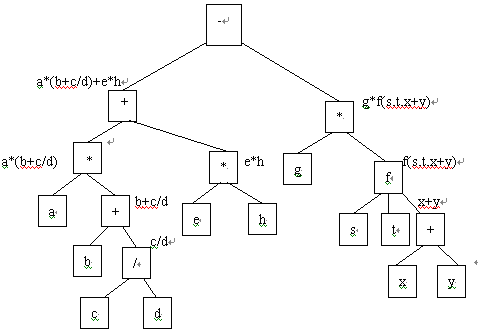
根据以上原则,可以将表达式
a*(b+c/d)+e*h-g*f(s,t,x+y) 用如图 1.29 来表示。表示表达式的树通常称为表达式树。由图 1.29 可以看出,表示一个表达式的表达式树是不唯一的,如上述表达式可以表达成图 1.29 ( a )和图 1.29 ( b )两种表达式树。
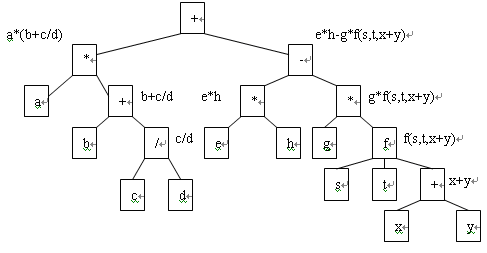
(a)
(b)
图1.29 a*(b+c/d)+e*h-g*f(s,t,x+y)表达式的两种表达式树
树在计算机中通常用多重链表表示。多重链表中的每个结点描述了树中对应结点的信息,而每个结点中的链域(即指针域)个数将随树中该结点的度而定,其一般结构如图 2.30 所示。

图1.30 树链表中的节点结构
在表示树的多重链表中,由于树中每个结点的度一般是不同的,因此,多重链表中各结点的链域个数也就不同,这将导致对树进行处理的算法很复杂。如果用定厂的结点来表示树中的每个结点,即取树的度作为每个结点的链表个数,这就可以使对树的各种处理算法大大简化。但在这种情况下,容易造成存储空间的浪费,因为有可能在很多结点中存在空链域。后面将介绍用二叉树表示一般的树,会给处理带来方便。
1.6.2 二叉树及其基本性质 
1.什么是二叉树
二叉树( binary tree )是一种很有用的非线性结构。二叉树不同于前面介绍的树结构,但它 3 与树结构很相似,并且,树结构的所有术语都可以用到二叉树这种数据结构上。
二叉树具有以下两个特点:
• 非空二叉树只有一个根结点;
• 每一个结点最多有两个子树,且分别称为该结点的左子树与右子树。
由以上特点可以看出,在二叉树中,每一个结点的度数最大为 2 ,即所有子树(左子数或右子树)也均为二叉树,而树结构中的每一个结点的度是任意的。另外,二叉树中的每一个结点的子树被明显地分为左子树和右子树。在二叉树中,一个结点可以只有左子树而没有右子树,也可以只有右子树而没有左子树。当一个结点既没有左子树也没有右子树,该结点即是叶子结点。
图 1.31 ( a )是一棵只有叶子结点的二叉树。图 1.31 ( b )是一棵深度是 4 的二叉树。
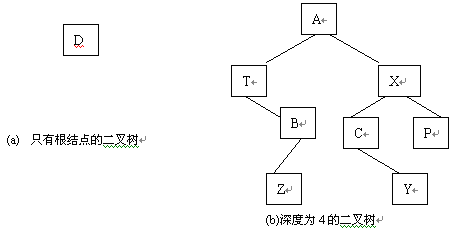
图1.31 二叉树的例
2. 二叉树的基本性质:
二叉树具有以下基本性质:
性质 1:在二叉树的 k 层上,最多有 2 k-1 (k ≥ 1) 个结点。根据二叉树的特点,这个性质是显然的。
性质 2: 深度为 m 的二叉树最多有 2 m -1 个结点。深度为 m 的二叉树是指二叉树共有 m 层。
根据性质 1 ,只要将第一层到第 m 层上的最大的结点树相加,就可以得到整个二叉树的最大值,即 2 1-1 +2 2-1 +…+ 2 m -1 = 2 m -1
性质 3: 在任意一棵二叉树中,度为 0 的结点(即叶子结点)总是比度为 2 的结点多一个。
对于这个性质说明如下:
假设二叉树中有 n 0 个叶子结点, n 1 个度为 1 的结点, n 2 个度为 2 的结点,则二叉树中总的结点数为
n=n 0 +n 1 +n 2
由于在二叉树中除了根结点外,其余每一个结点都有惟一的一个分支进入;设二叉树中所有进入分支的总数为 m ,则二叉树中总的结点数为
n=m+1
又由于二叉树中树中这 m 个进入分支是分别由非叶子结点射出的。其中度为 1 的每个结点射出 1 个分支,度为 2 的每个结点射出 2 个分支。因此,二叉树所有度为 1 与度为 2 的结点射出的分支总数为 n 1 +2n 2 。而在二叉树中,总的射出分支数应与总的进入分支数相等,即
m= n 1 +2n 2
将( 3 )代入( 2 )式有
n= n 1 +2n 2 +1
最后比较( 1 )式和( 4 )式有
n 0 +n 1 +n 2 = n 1 +2n 2 +1
化简后得
n 0 =n 2 +1
即:在二叉树中,度为 0 的结点(即叶子结点)总是比度为 2 的结点多一个。
例如,在图 1.31(b) 所示的二叉树中,有 3 个叶子结点,有 2 个度为 2 的结点,度为 0 的结点比度为 2 的结点多一个。
性质 4: 具有 n 个结点的二叉树,其深度至少为 [log 2 n] +1 ,其中 [log 2 n] 表示取 log 2 n 的整数部分。
这个性质可以由性质 2 直接得到。
3 .满二叉树与完全二叉树
满二叉树与完全二叉树是两种特殊的二叉树。
·满二叉树
所谓满二叉树是指这样的一种二叉树:除最后一层外,每一层上的所有结点都有两个叶子结点。这就是说,在满二叉树中,每一层上的结点数都达到最大值,即在满二叉树的第 k 层上有 2 k-1 个结点,且深度为 m 的满二叉树有 2 m -1 个结点。
图 1.32(a) 、 1.32(b) 、 1.32(c) 、分别是深度为 2 、 3 、 4 的满二叉树。
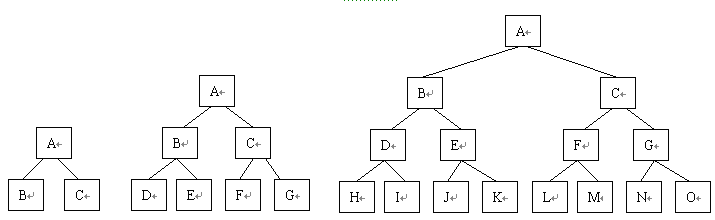
图1.32 满二叉树
·完全二叉树
所谓完全二叉树是指这样的二叉树:除最后一层外,每一层上的结点数均达到最大值;在最后一层上只缺少有右边的若干结点。
更确切地说,如果从根结点起,对二叉树的结点自上而下、自左至右用自然数进行连续编号,则深度为 m 、且有 n 个结点的二叉树,当且仅当其每一个结点都与深度为 m 的满二叉树中编号从 1 到 n 的结点一一对应时,称之为完全二叉树。
图 1.33 ( a )、 1.33 ( b )分别是深度为 3 、 4 的完全二叉树。
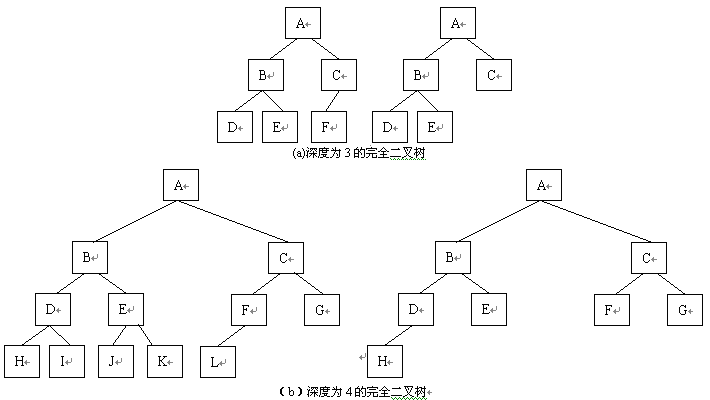
图1.33 完全二叉树
对于完全二叉树来说,叶子结点只可能在层次最大的两层上出现,对于任何一个结点,若其右分支下的子孙结点的最大 层次为 p ,则其左分支下的子孙结点的最大层次为 p ,或为 p+1 。
由满二叉树与完全二叉树的特点可以看出,满二叉树也是完全二叉树,而完全二叉树一般不是满二叉树。
完全二叉树还具有以下两个性质:
性质 5 :具有个结点的完全二叉树的深度为 [log 2 n] +1.
性质 6: 设完全二叉树共有 n 结点。如果从根结点开始,按层序(每一层从左到右)用自然数 1 , 2 , …, n 给结点编号,则对于编号为 k(k=1,2,…, n) 的结点有以下结论:
• 若 k=1 ,则该结点为 k 的结点,它没有父结点;若 k>1 ,则该结点的父结点编号为 INT(k/2) 。
• 若 2k ≤ n ,则编号为 k 的结点的左子结点编号为 2k ;否则该结点无左子结点(显然也没有右子结点)。
• 若 2k+1 ≤ n ,则编号为 k 的结点的右子结点编号为 2k+1 ;否则该结点无右子结点。
根据完全二叉树的这个性质,如果按 从上到下,从左到右顺序存储完全二叉树的各结点,则很容易确定每一个结点的父结点,左子结点和右子结点的位置
1.6.3 二叉树的存储结构

在计算机中,二叉树通常采用链式存储结构。
与线性链表类似,用于存储二叉树中各元素的存储结点也由两部分组成;数据域与指针域。但在二叉树中,由于每一个元素可以有两个后件(即两个子结点),因此,用于存储二叉树的存储结点的指针域有两个; 一个用于指向该结点的左子结点的存储地址,称为左指针域,另一个用于指向该结点的右子结点的存储地址,称为右指针域。图 1.34 为二叉树的存储结点示意图。其中, L(i) 为结点 i 的左指针域,即 L(i) 为结点 i 的左子结点的存储地址, R(i) 为结点 i 的右指针域,即 R(i) 为结点 i 的右子结点的存储地址, V(i) 为数据域。
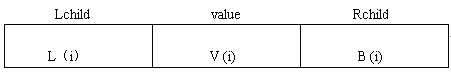
图1.34 二叉树存储节点的结构
由于二叉树的存储的存储结构中每一个存储结点有两个指针域,因此,二叉树的链式存储结构也称为二叉链表。图 1.35(a), 1.35(b), 1.35(c) 分别表示了一棵二叉树,二叉树链表的逻辑状态,二叉树链表的物理状态,其中 BT 称为二叉链表的头指针,用于指向二叉树根结点(即存放二叉树根结点的存储地址)。
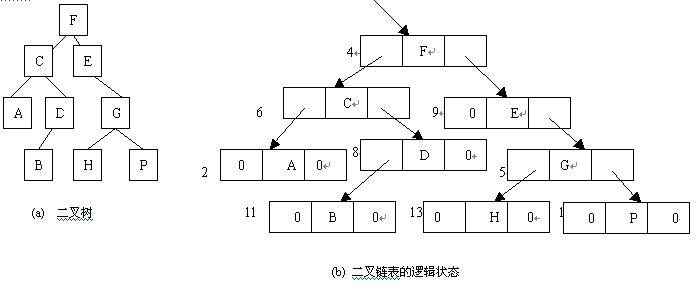
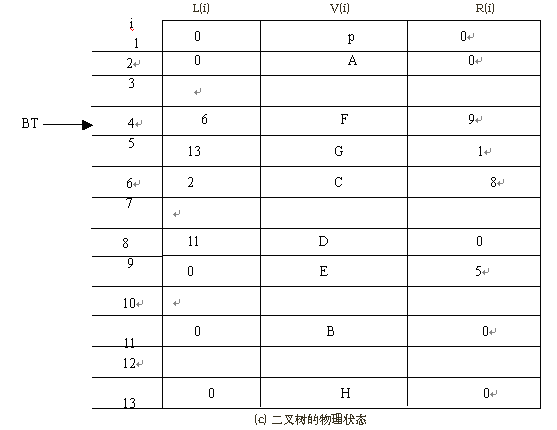
图 1.35 二叉树的链式存储结构
对于满二叉树与完全二叉树来说,根据完全二叉树的性质 6 ,可以按层序进行顺序存储,这样,不仅节省了存储空间,又能方便地确定每一个结点的父结点与左右子结点的位置,但顺序存储结构对于一般的二叉树不适用。
1.6.4 二叉树的遍历 
由于二叉树是一种是非线性结构,因此,对二叉树的遍历要比遍历线性表复杂的多。在遍历二叉树的过程中,当访问到某个结点是,再往下访问可能有两个分支,那么先访问哪一个分支呢?对于二叉树来说,需要访问根结点,左子树上的所有结点,右子树上的所有结点,在这三种中,究竟先访问哪一个?也就是说,遍历二叉树的方法实际上是要确定访问各结点的顺序,以便不重不漏地访问到二叉树中的所有结点。
在遍历二叉树的过程中,一般先 遍历左子树,然后再遍历右子树。在先左后右的原则下,根据访问根结点的次序二叉树遍历可以分为三种:前序遍历,中序遍历,后序遍历。下面分别介绍这三种遍历的方法。
• 前序遍历( DLR )
所谓前序遍历是指在访问根结点,遍历左子树与遍历右子树这三者中,首先访问根结点,然后遍历左子树,最后遍历右子树;并且,在遍历左,右子树时,仍然先访问根结点,然后遍历左子树,最后遍历右子树。因此,前序遍历二叉树的过程是一个递归的过程。
下面是二叉树前序遍历的简单描述:
若二叉树为空,则结束返回。
否则: (1)访问根结点;
(2)前序遍历左子树;
(3)前序遍历右树;
在此特别要注意的是,在遍历右子树时仍然采用前序遍历的方法。如果对图 1.35(a) 中的二叉树进行前序遍历,则遍历的结果为 F, C, A, D, B, E, G, H, P (称为该二叉树的前序序列)。
• 中序遍历( LDR )
所谓前序遍历是指在访问根结点,遍历左子树与遍历右子树这三者中,首先遍历左子树,然后访问根结点,最后遍历右子树;并且,在遍历左,右子树时,仍然先访问遍历左子树,然后根结点,最后遍历右子树。因此,中序遍历二叉树的过程也是一个递归的过程。
下面是二叉树中序遍历的简单描述:
若二叉树为空,则结束返回。
否则:(1)中序遍历左子树;
(2)访问根结点;
(3)中序遍历左子树;
在此特别要注意的是,在遍历左右子树时仍然采用中序遍历的方法。如果对图 1.35(a) 中的二叉树进行中序遍历,则遍历的结果为 A, C, B, D, F, E, H, G, P (称为该二叉树的中序序列)。
• 后序遍历( LRD )
所谓后序遍历是指在访问根结点,遍历左子树与遍历右子树这三者中,首先遍历左子树,然后遍历右子树,最后访问根结点;并且,在遍历左,右子树时,仍然先访问遍历左子树,然后遍历右子树,最后访问根结点。因此,后序遍历二叉树的过程也是一个递归的过程。
下面是二叉树后序遍历的简单描述:
若二叉树为空,则结束返回。
否则:(1)后序遍历左子树;
(2)后序遍历右子树;
(3)访问根结点;
在此特别要注意的是,在遍历左右子树时仍然采用后序遍历的方法。如果对图 1.35(a) 中的二叉树进行后序遍历,则遍历的结果为 A, B, D, C, H, P, G, E, F (称为该二叉树的后序序列)。