1.3.1 线性表的基本概念
　　1.3.2 线性表的顺序存储结构
　　1.3.3 顺序表的插入运算
　　1.3.4 顺序表的删除运算

　　1.3.1 什么是数据结构　

　　线性表（ Linear List ）是最简单、最常用的一种数据结构。
　  线性表由一组数据元素构成。数据元素的含义很广泛，在不同的具体情况下，它可以有不同的含义。例如，一个 n 维向量（ x 1 ,x 2 ,…,x n ）是一个长度为 n 的线性表，其中的每一个分量就是一个数据元素。又如，英文小写字母表（ a,b,c,…,z ）是一个长度为 26 的线性表，其中的每一个小写字母就是一个数据元素。再如，一年中的四个季节（春，夏，秋，冬）是一个长度为 4 的线性表，其中的每一个季节名就是一个数据元素。
　  矩阵也是一个线性表，只不过它生意一个比较复杂的线性表。在矩阵中，既可以把每一行看成是一个数据元素（即一个行向量为一个数据元素），也可以把每一个列看成是一个数据元素（即一个列向量为一个数据元素）。其中每一个数据元素（一个行向量或列向量）实际上又是一个简单的线性表。
　  数据元素可以是简单项（如上述例子中的数、字母、季节名等）。在稍微复杂的线性表中，一个数据元素还可以由若干个数据项组成。例如，某班的学生情况登记表是一个复杂的线性表，表中每一个学生的情况就组成了表中的每一个元素，每一个数据元素包括姓名、学号、性别、年龄和健康状况 5 个数据项，如表 1.6 所示。在这种复杂的线性表中，由若干个数据项组成的数据元素称为记录（ record ），而由多个记录组成的线性表又称为文件（ file ）。因此，上述学生情况登记表就是一个文件，其中每一个学生的情况就是一个记录。
　　　　　　
　　　　　　　　　　　　　　　　　　　　　　　　表1.6　学生情况登记表

　  综上所述，线性表是由 N （ N>=0 ）个数据元素 a1,a2…….,an 组成的一个有限序列，表中的每一个数据元素，除了第一个外，有一个前件，除了最后一个外，有且有一个后件。即线性表或是一个空表，或可以表示为
　　 （ a1,a2,…ai,…,an ）
　  其中是属于数据对象的元素，通常也称其为线性表中的一个结点。
　  显然线性表是一种线性结构。数据元素在线性表中的位置只取决于它们自己的序号，即数据元素之间的相对位置是线性的。
　  非空线性表有如下一些结构特征：
　   ·有且只有一个根结点 a1 ，它无前件。
　   ·有且只有一个终点 an ，它无前件。
　   ·除根结点与终端结点外，其他所有结点有且只有一个前件，也有且只有一个后件。线性表中结点的个数 n 称为线性表的产妇度。当 n=0 时，称为空表。

　　1.3.2 线性表的顺序存储结构

　　在计算机中存放线性表，一中最简单的方法是顺序存储，也称为顺序分配。
　  线性表的顺序存储结构具有以下两个基本特点：
　  · 线性表中所有元素所占的存储空间是连续的
 　 · 线性表中各数据元素在存储空间中是按逻辑顺序依次存放的
　  由此可以看出，在线性表的顺序结构中，其前后件两个元素在存储空间中是紧邻的，且前件元素一定存储在后件元素的前面。
　  在线性表的顺序存储结构中，如果线性表中各数据元素所占的存储空间（字节数）相等，则在该线性表中查找某一个元素是很方便的。
　  假设线性表中的第一个数据元素的存储地址（指第一个字节的地址，即首地址）为 ADR （ a1 ），每一个数据元素占 k 个字节，则线性表中第 i 个元素 ai 在计算机存储空间中的存储地址为
　  ADR(ai)=ADR(a1)+(i-1)k
　  即在顺序存储结构中，线性表中每一个数据元素在计算机存储空间中的存储地址由该元素在线性表中的位置序号唯一确定。一般来说，长度为 n 线性表
　  （ a1,a2,…ai,…,an ）
　  在计算机中的顺序存储结构如图 1.6 所示。
　　　　　　　　　　　　　　　　　　　　　
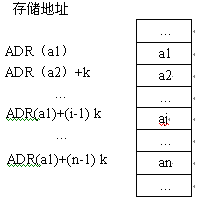
　　　　　　　　　　　　　　　　　　　　　　图 1.6 线性表的顺序存储结构
　　在程序设计语言中，通常定义一个一维数组来表示线性表的顺序存储空间。因为程序设计语言中的一维数组与计算机中实际的存储空间结构是类似的，这就便于用程序设计语言对线性表进行各种运算处理 。
　  在用一维数组 存放线性表时，该一维数组的长度通常要定义得比线性表的实际长度大一些，以便对线性表进行各种运算，特别是插入运算。在一般情况下，如果线性表的长度在处理过程中是动态变化的，则在开辟线性表的存储空间是要考虑到线性表在动态变化过程中可能达到的最大长度。如果开始时所开辟的存储空间太小，则在线性表动态增长时可能会出现存储空间不够而无法再插入新的元素；但如果开始时开辟的存储空间太大，而实际上又用不着那么大的存储空间，则会造成存储空间的浪费。在实际应用中，可以根据线性表动态变化过程中的一般规模来决定开辟的存储空间量。
　  在线性表的顺序存储结构下，可以对线性表进行各种处理。主要的运算有以下集中：
　　·在线性表的指定位置处假如一个新的 ( 即线性表的插入 ) ；
　　·在线性表中删除指定的元素（即线性表的排序）；
　　·在线性表中查找某个（或某些）特定的元素（即线性表的查找）；
　　·对线性表的元素进行整序（即线性表的排序）；
　　·按要求将一个线性表分解成多个线性 ( 即线性表的分解 ) ；
　　·按要求将多哥线性表合并成一个线性表（即线性表的合并）；
　　·复制一个线性表（即线性表的复制）；
    ·逆转一个线性表（即线性表的逆转）等。
　  下面两小节主要讨论线性表在顺序存储结构下的插入与删除问题。

　　1.3.3 顺序表的插入运算

　　首先举一个例子来说明如何在顺序存储结构的线性表中插入一个新元素。
　  例 1.9 图 1.7 （ a ）为一个长度为 8 的线性表顺序存储在长度为 10 的存储空间中现在要求在第 2 个元素（即 18 ）之前插入一个新元素 87 。其插入过程如下：
　   首先从最后一个元素开始直到第 2 个元素，将其中的每一个元素均依次往后移动一个位置，然后将新元素 87 插入到第 2 位置。
　  插入一个新元素后，线性表的长度变成了 9 ，如图 1.7 （ b ）所示。
　  如果再要在线性表的第 9 个元素之前插入一个新元素 14 ，则采用类似的方法：将第 9 个元素往后移动一个位置，然后将新元素插入到第 9 个位置。插入后，线性表的长度变成了 10 ，如图 1.7 （c）所示。
　  现在，为线性表开辟的存储空间已经满了，不能再插入新的元素了。如果再要插入，则会造成称为“上溢”的错误。
　　　　　
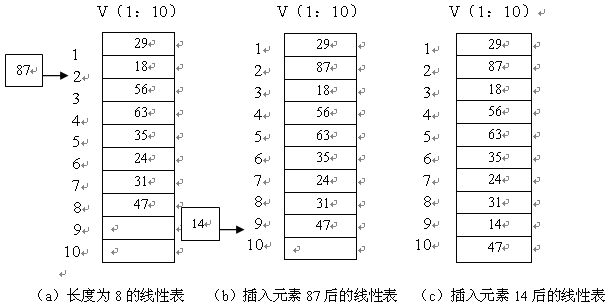
　　　　　　　　　　　　　　　　　　　　　　　图1.7 线性表在顺序存储结构下的插入
　　一般来说，没长度为 n 的线性表为
　 （ a1,a2,…,ai,…,an ）
　  现要在线性表的第 i 个元素 ai 之前插入一个新元素 b ，插入后得到长度为 n+1 的线性表为 （ a 1' ,a 2' ,…aj',aj+ 1' ,…,an',an+ 1' ）
　  则插入前后的两线性表中的元素满足如下关系：
　　 aj 1<=j<=i-1
　　 aj= b j=i
　　 aj-1 i+1<=j<=n+1
　　在一般情况下，要在第 i(1<=i<=n) 个元素之前插入一个新元素时，首先要从最后一个（即第 n 个）元素开始，直到第 i 个元素之间共 n-i+1 个元素依次向后移动一个位置，移动结束后，第 i 个位置就被空出，然后将新元素插入到第项。插入结束后，线性表的长度就增加了 1 。
　  显然，在线性表表采用顺序存储结构时，如果插入运算在线性表末尾进行，即在第 n 个元素之后（可以认为是在第 n+1 个元素之前）插入新元素，则只要在表的末尾增加一个元素即可，不需要移动表中的元素；如果要在线性表的第 1 个元素之前插入一个新元素，则需要移动表中所有的元素。在一般情况下，如果插入运算在第 i(1<=i<=n) 个元素之前进行，则原来地个元素 i 之后（包括第 i 个元素）的所有元素都必须移动。在平均情况下，要在线性表中插入新元素，需要一送表中一半的元素。因此，在线性表顺序存储的情况下，要插入一个新元素，其效率是很地的，特别是在线性表比较大的情况下更为突出，由于数据元素的移动而消耗较多的处理时间。

1.3.4 顺序表的删除运算　

　  首先举一个例子来说明如何在顺序存储结构的线性表中删除元素。
　   例 1.10 图 1.8 （ a ）为一个长度为 8 的线性顺序存储在长度为 10 的存储空间中。现在要求删除线性表中的第 1 个元素（即删除元素 290 。其删除过程如下：
　   从第 2 个元素开始直到最后一个元素，将其中的每一个元素均依次往前移动一个位置。此时，线性表的长度变成了 7 ，如图 1.8 （ b ）所示。
　  如果再要删除线性表中的第 6 个元素，则采用类似的方法：将第 7 个元素往前移动一个位置。此时，线性表的长度成了 6 ，如图 1.8 （ c ）所示。
　　　　　
　　　　　　　　　　　　　　　　　　　　　　图1.8　线性表在顺序存储结构下的删除
　　一般来说，设长度为 n 的线性表为
　  (a1,a2,…,ai,…,an)
　  现要删除第 i 个元素，删除后得到长度为 n-1 的线性表为
　  （ a 1' ,a 2' ,…aj', …,an -1' ）
　  则删除前后的两线性表中的元素满足如下关系：
　　 aj 1<=j<=i-1
　　 aj ‘ =
　　 aj+1 i<=j<=n-1
　  在一般情况下，要删除第 i(1<=i<=n) 个元素时，则要从第个元素开始，直到第 n 个元素之间共 n-i 个元素依次向前移动一位置。删除结构后，线性表的长度就减小了 1 。
　  显然，在线性表采用消魂许存储结构时，如果删除运算在线性表的末尾进行，即删除第 n 个元素，则不需要移动表中的元素；如果要删除线性表中的第 1 个元素，则需要移动表中所有的元素。在一般情况下，如果要删除第 i(1<=i<=n) 个元素，则原来第 i 个元素之后的所有元素都必须依次往前移动一个位置。在平均情况下，要在线性表中删除一个元素，需要移动表中一半的元素。因此，在线性表顺序存储的情况下，要删除一个元素，其效率也是很低的特别是在线性表比较大的情况下更为突出，由于数据元素的移动而消耗较多的处理时间。
　  由线性表在顺序存储结构下的插入与删除运算可以看出，线性表的顺序存储结构对于小线性表或者其中元素不常变动的线性表来说是合适的，因为顺序存储的结构比较简单。
　  但这种顺序存储的方式对于元素经常需要变动的大线性表就不太合适了，因为插入与删除的效率比较低。