利用计算机进行数据处理是计算机应用的一个重要领域。在进行数据处理时,实际需要处理的数据元素一般有很多,而这些大量的数据元素都需要存放在计算机中,因此,大量的数据元素在计算机中如何组织,以便提高数据处理的效率,并且节省计算机的存储空间,这是进行数据处理的关键问题。
显然,杂乱无章的数据是不便于处理的。而将大量的数据随意地存放在计算机中,实际上也是“自找苦吃”,对数据处理更是不利。
数据结构作为计算机的一门学科,主要研究和讨论以下三个方面的问题:
① 数据集合中各数据元素之间所固有的逻辑关系,即数据的逻辑结构;
② 在对数据进行处理时,各数据元素在计算机中的存储关系,即数据的存储结构;
③ 对各种数据结构进行的运算。
讨论以上问题的主要目的是为了提高数据处理的效率。所谓提高数据处理的效率,主要包括两个方面:一是提高数据处理的速度,二是尽量节省在数据处理过程中所占用的计算机存储空间。
本章主要讨论工程上常用的一些基本数据结构,它们是软件设计的基础。
1.2.1 什么是数据结构
1.2.2 数据结构的图形表示
1.2.3 线性结构与非线性结构
1.2.1
什么是数据结构 
计算机已被广泛用于数据处理。实际问题中的各数据元素之间总是相互关联的。所谓数据处理,是指对数据集合中的各元素以各种方式进行运算,包括插入、删除、查找、更改等运算,也包括对数据元素进行分析。在数据处理领域中,建立数据模型有时并不十分重要,事实上,许多实际问题是无法表示成数学模型的。人们最感兴趣的是知道数据集合中各数据元素之间存在什么关系,应如何组织它们,即如何表示所需要处理的数据元素。
下面通过两个实例来说明对同一批数据用不同的表示方法后,对处理效率的影响。
例 1 . 3 无序表的顺序查找与有序表的对分查找。
图 1.1 是两个子表。从图中可以看出,在这两个子表中所存放的数据元素是相同的,但它们在表中存放的顺序是不同的。在图 1.1 ( a )所示的表中,数据元素的存放顺序是没有规则的;而在图 1.1(b) 所示的表中,数据元素是按从小到大的顺序存放的。我们称前者为无序表,后者为有序表。

无序表
有序表
图1.1 存放顺序不同的两个表
下面讨论在这两种表中进行查找的问题。
首先讨论在图 1.1(a) 所示的无序表中进行查找。由于在图 1.1(a) 表中数据元素的存放顺序没有一定的规则,因此,要在这个表中查找某个数时,只能从第一个元素开始,逐个将表中的元素与被查数进行比较,直到表中的某个元素与被查数相等(即查找成功)或者表中所有元素与被查数都进行了比较且都不相等(即查找失败)为止。这种查找方式称为顺序查找。显然,在顺序查找中,如果被查找数在表的前部,则需要比较的次数就少;但如果被查找数在表的后部,则需要比较的次数就多。特别是当被查数刚好是表中的第一个元素时(如被查数为 35 ),只需要比较一次就查找成功;但当被查数刚好是表中最后一个元素(如被查数为 46 )或表中根本就没有被查数时(如被查数为 67 ),则需要与表中所有的元素进行比较,在这种情况下,当表很大时,顺序查找是很费时间的。虽然顺序查找法的效率比较低,但由于图 1.1(a) 为无序表,没有更好的查找方法,只能顺序查找。
现在再讨论在图 1.1(b) 所示的有序表中进行查找。由于有序表中的元素是从小到大进行排列的,在查找时可以利用这个特点,以便使比较次数大大减少。在有序表中查找一个数可以如下进行:
将被查数与表中的中间元素进行比较:若相等,则表示查找成功,查找过程结束;若被查数大于表中的这个中间元素时,则表示如果被查数在表中的话,只能在表的后半部,此时可以抛弃表的前半部而保留后半部;若被查数小于表中的这个中间元素,则表示如果被查数在表中的话,只能在表的前半部,此时可以抛弃表的后半部而保留前半部。然后对剩下的部分(前半部或后半部)再按照上述方法进行查找,这个过程一直做到在某一次的比较中相等(查找成功)或剩下的部分已空(查找失败)为止。例如,如果要在图 1.1(b) 所示的有序表中查找 54 ,则首先与中间元素 35 进行比较,由于 54 大于 35 ,再与后半部分的中间元素 54 进行比较,此时相等,共比较了 2 次就查找成功。如果采用顺序查找法,在图 1.1(a) 所示的无序表中查找 54 这个元素,需要比较 9 次。这种查找方法称为有序表的对分查找。
显然,在有序表的对分查找中,不论查找的是什么数,也不论要查找的数在表中有没有,都不需要与表中所有的元素进行比较,只需要与表中很少的元素进行比较。但需要指出的是,对分查找只适用于有序表,而对于无序表是无法进行对分查找的。
实际上,在日常工作和学习中也经常遇到对分查找。例如,当需要在词典中查找一个单词时,一般不是从第一页开始一页一页的往后找,而是考虑到词典中的各单词是以英文字母为顺序排列的,因此可以根据所查单词的第一个字母,直接翻到大概位置,然后进行比较,根据比较结果再向前或向后翻,直到找到该单词为止。这种在词典中查单词的方法类似于对分查找。
由这个例子可以看出,数据元素在表中的排列顺序对查找效率是有很大影响的。
例 1 . 4 设有一学生情况登记表如表 1.1 所示。在表 1.1 中,每个学生的情况是以学号为顺序排列的。
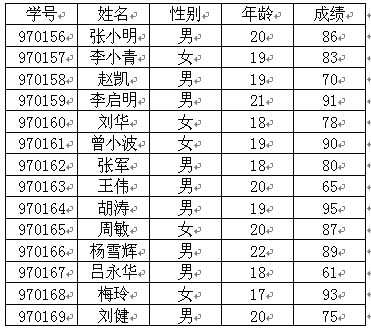
表1.1 学生情况登记表
显然,如果要在表 1.1 中查找给定学号的某学生的情况是方便的,只要根据给定的学号就可以立即找到该学生的情况。但是,如果要在该表中查找成绩在 90 分以上的所有学生的情况,则需要从头到尾扫描全表,才能将成绩在 90 分以上的所有学生找到。在这种情况下,为了找到成绩在 90 分以上的学生情况,对于成绩在 90 分以下的所有学生情况也都要被扫描到。由此可以看出,要在表 1.1 中查找给定学号的学生情况虽然很方便,但要查找成绩在某个分数段中的学生情况时,实际上需要查看表中所有学生的成绩,其效率是很低的,尤其是当表很大时更为突出。
为了便于查找成绩在某个分数段中的学生情况,可以将表 1.1 中所登记的学生情况进行重新组织。例如,将成绩在 90 分以上(包括 90 分,下同)、 80~89 分、 70~79 分、 60~69 分之间的学生情况分别登记在四个独立的子表中,分别如表 1.2 、表 1.3 、表 1.4 与表 1.5 所示。现在如果要查找 90 分以上的所有学生的情况,就可以直接在表 1.2 中进行查找,从而避免了对成绩在 90 分以下的学生情况的扫描,提高了查找效率。

表1.2 成绩90以上学生情况登记表 |

表1.3 成绩80-90间学生情况登记表 |
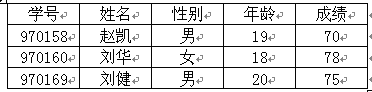

表1.4 成绩70-79间学生情况登记表 表1.4 成绩60-69间学生情况登记表
由例 1.4 可以看出,在对数据进行处理时,可以根据所做的运算不同,将数据组织成不同的形式,以便于做该种运算,从而提高数据处理的效率。
简单的说,数据结构是指相互有关联的数据元素的集合。例如,向量和矩阵就是数据结构,在这两个数据结构中,数据元素之间有着位置上的关系。又如,图书馆中的图书卡片目录,则是一个较为复杂的数据结构,对于列在各卡片上的各种书之间,可能在主题、作者等问题上相互关联,甚至一本书本身也有不同的相关成分。
数据元素具有广泛的含义。一般来说,现实世界中客观存在的一切个体都可以是数据元素。例如:
描述一年四季的季节名
春、夏、秋、冬
可以作为季节的数据元素;
表示数值的各个数
18 、 11 、 35 、 23 、 16 、 ...
可以作为数值的数据元素;
表示家庭成员的各成员名
父亲、儿子、女儿
可以作为家庭成员的数据元素。
甚至每一个客观存在的事件,每一次演出、一次借书、一次比赛等也可以作为数据元素。
总之,在数据处理领域中,每一个需要处理的对象都可以抽象成数据元素。数据元素一般简称为元素。
在实际应用中,被处理的数据元素一般有很多,而且,作为某种处理,其中的数据元素一般具有某种共同特征。例如, { 春,夏,秋,冬 } 这四个数据元素有一个共同特征,即它们都是季节名,分别表示了一年中的四个季节,从而这四个数据元素构成了季节名的集合。又如, { 父亲,儿子,女儿 } 这三个数据元素也有一个共同特征,即它们都是家庭的成员名,从而构成了家庭成员名的集合。一般来说,人们不会同时处理特征完全不同且互相之间没有任何关系的各类数据元素,对于具有不同特征的数据元素总是分别进行处理。
一般情况下,在具有相同特征的数据元素集合中,各个数据元素之间存在有某种关系(即联系),这种关系反映了该集合中的数据元素所固有的一种结构。在数据处理领域中,通常把数据元素之间这种固有的关系简单的用前后件关系(或直接前驱与直接后继关系)来描述。
例如,在考虑一年四个季节的顺序关系时,则“春”是“夏”的前件(即直接前驱,下同),而“夏”是“春”的后件(即直接后继,下同)。同样,“夏”是“秋”的前件,“秋”是“夏”的后件;“秋”是“冬”的前件,“冬”是“秋”的后件。
在考虑家庭成员间的辈分关系时,则“父亲”是“儿子”和“女儿”的前件,而“儿子”与“女儿”都是“父亲”的后件。
前后件关系是数据元素之间的一个基本关系,但前后件关系所表示的实际意义随具体对象的不同而不同。一般来说,数据元素之间的任何关系都可以用前后件关系来描述。
1 .数据的逻辑结构
前面提到,数据结构是指反映数据元素之间关系的数据元素集合表示。更通俗的说,数据结构是指带有结构的数据元素的集合。在此,所谓机构实际上就是指数据元素之间的前后件关系。
由上所述,一个数据结构应包含以下两方面的信息;
① 表示数据元素的信息;
② 表示各数据元素之间的前后件关系。
在以上所述的数据结构中,其中数据元素之间的前后件关系是指它们的逻辑关系,而与它们在计算机中的存储位置无关。因此,上面所述的数据结构实际上是数据的逻辑结构。
所谓数据的逻辑结构,是指反映数据元素之间逻辑关系的数据结构。
由前面的叙述可以知道,数据的逻辑结构有两个要素:一是数据元素的集合,通常记为 D ;二是 D 上的关系,它反映了 D 中各数据元素之间的前后件关系,通常记为 R 。即一个数据结构可以表示成
B= ( D , R )
其中 B 表示数据结构。为了反映 D 中各数据元素之间的前后件关系,一般用二元组来表示。例如,假设 a 与 b 是 D 中的两个数据,则二元组 (a,b) 表示 a 是 b 的前件, b 是 a 的后件。这样,在 D 中的每两个元素之间的关系都可以用这种二元组来表示。
例 1 . 5 一年四季的数据结构可以表示成
B= ( D , R )
D={ 春,夏,秋,冬 }
R={ (春,夏),(夏,秋),(秋,冬) }
例 1.6 家庭成员数据结构可以表示成
B= ( D , R )
D={ 父亲,儿子,女儿 }
R={ (父亲,儿子),(父亲,女儿) }
例 1.7 n 维向量
X= ( x 1 ,x 2 ,…,x n )
也是一种数据结构。即 X= ( D , R ),其中数据元素的集合为
D={x 1 ,x 2 ,…,x n }
关系为
R={(x 1 ,x 2 ),(x 2 ,x 1 )…,(x n-1 ,x n )}
对于一些复杂的数据结构来说,它的数据元素可以是另一种数据结构。
例如, m×n 的矩阵
a 11 a 12 … a 1n
a 21 a 22 … a 2n
. . .
. . .
. . .
a m1 a m2 … a mn
是一个数据结构。在这个数据结构中,矩阵的每一行
A i =(a i1 ,a i2 ,…,a in ),i=1,2,…,m
可以看成是它的一个数据元素。即这个数据结构的数据元素的集合为
D={A 1 , A 2 , … , A m }
D 上的一个关系为
R={(A 1 ,A 2 ),(A 2 ,A 3 ),…,(A i ,A i+1 ),…,(A m-1 ,A m )}
显然,数据结构 A 中的每一个数据元素 A i ( i=1,2,…,m )又是另一个数据结构,即数据元素的集合为 D i 上的一个关系为
R i ={(a i1 ,a i2 ),(a i2 ,a i3 ),…,(a ij ,a i,j+1 ),…,(a i,n-1 ,a in )}
2 .数据的存储结构
数据处理是计算机应用的一个重要领域,在实际进行数据处理时,被处理的各数据元素总是被存放在计算机的存储空间中,并且,各数据元素在计算机存储空间中的位置关系与它们的逻辑关系不一定是相同的,而且一般也不可能相同。例如,在前面提到的一年四个季节的数据结构中,“春”是“夏”的前件,“夏”是“春”的后件,但在对它们进行处理时,在计算机存储空间中,“春”这个数据元素的信息不一定被存储在“夏”这个数据元素信息的前面,而可能在后面,也可能不是紧邻在前面,而是中间被其他的信息所隔开。又如,在家庭成员的数据结构中,“儿子”和“女儿”都是“父亲”的后件,但在计算机存储空间中,根本不可能将“儿子”和“女儿”这两个数据元素的信息都紧邻存放在“父亲”这个数据元素信息的后面,即在存储空间中与“父亲”紧邻的只可能是其中的一个。由此可以看出,一个数据结构中的各数据元素在计算机存储空间中的位置关系与逻辑关系是有可能不同的。
数据的逻辑结构在计算机存储空间中的位置关系与逻辑关系是有可能不同的。
由于数据元素在计算机存储空间中的位置关系可能与逻辑关系不同,因此,为了表示存放在计算机存储空间中的各数据元素之间的逻辑关系(即前后件关系),在数据的存储结构中,不仅要存放各数据元素的信息,还需要存放各数据元素之间的前后件关系的信息。
一般来说,一种数据的逻辑结构根据需要可以表示成多种存储结构,常用的存储结构有顺序、链接、索引等存储结构。而采用不同的存储结构,其数据处理的效率是不同的。因此,在进行数据处理时,选择合适的存储结构是很重要的。
1 . 2 . 2 数据结构的图形表示 
一个数据结构除了用二元关系表示外,还可以直观的用图形表示。在数据结构的图形表示中,对于数据集合 D 中的每一个数据元素用中间标有元素值的方框表示,一般称之为数据结点,并简称为结点;为了进一步表示各数据元素之间的前后件关系,对于关系 R 中的每一个二元组,用一条有向线段从前件结点指向后件结点。
例如,一年四季的数据结构可以用如图 1.2 所示的图形来表示。
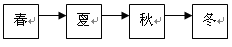
图1.2 一年四季数据结构的图形表示
又如,反映家庭成员间辈分关系的数据结构可以用如图 1.3 所示的图形表示。
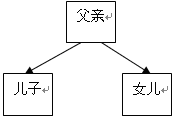
图1.3 家庭成员辈分关系数据结构的图形表示
显然,用图形方式表示一个数据结构是很方便的,并且比较直观。有时在不会引起误会的情况下,在前件结点到后件结点连线上的箭头可以省去。例如,在图 1.3 中,即使“父亲”结点与“儿子”结点连线上的箭头以及“父亲”结点与“女儿”结点连线上的箭头都去掉,同样表示了“父亲”是“儿子”与“女儿”的前件,“儿子”与“女儿”均是“父亲”的后件,而不会引起误会。
例 1.8 用图形表示数据结构 B= ( D , R ),其中
D={d i |1≤i≤7}={d 1 ,d 2 ,d 3 ,d 4 ,d 5 ,d 6 ,d 7 }
R={(d 1 ,d 3 ),(d 1 ,d 7 ),(d 2 ,d 4 ),(d 3 ,d 6 ),(d 4 ,d 5 )}
这个数据结构的图形表示如图 1.4 所示。
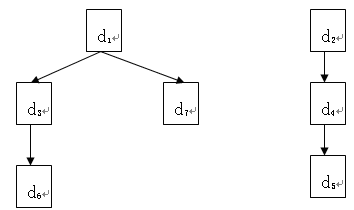
图1.4 例1.8中的数据结构
在数据结构中,没有前件的结点称为根结点;没有后件的结点称为终端结点(也称为叶子结点)。例如,在图 1.2 所示的数据结构中,元素“春”所在的结点(简称为结点“春”,下同)为根结点,结点“冬”为终端结点;在图 1.3 所示的数据结构中,结点“父亲”为根结点,结点“儿子”与“女儿”均为终端结点;在图 1.4 所示的数据结构中,有两个根结点 d 1 与 d 2 ,有三个终端结点 d 6 、 d 7 、 d 5 。数据结构中除了根结点与终端结点外的其它结点一般称为内部结点。
通常,一个数据结构中的元素结点可能在动态变化的。根据需要或在处理过程中,可以在一个数据结构中增加一个新结点(称为插入运算),也可以删除数据结构中的某个结点(称为删除运算)。插入与删除是对数据结构的两种基本运算,除此之外,对数据结构的运算还有查找、分类、合并、分解、复制和修改等。在对数据结构的处理过程中,不仅数据结构中的结点(即数据元素)个数在动态的变化,而且,各数据元素之间的关系也有可能在动态的变化。例如,一个无序表可以通过排序处理而变成有序表;一个数据结构中的根结点被删除后,它的某一个后件可能就变成了根结点;在一个数据结构中的终端结点后插入一个新结点后,则原来的那个终端结点就不再是终端结点而成为内部结点了。有关数据结构的基本运算将在后面讲到具体数据结构时再介绍。
1 . 2 . 3 线性结构与非线性结构 
如果在一个数据结构中一个数据元素都没有,则称该数据结构为空的数据结构。在一个空的数据结构中插入一个新的元素后就变为非空;在只有一个数据元素的数据结构中,将该元素删除后就变为空的数据结构。
根据数据结构中各数据元素之间前后件关系的复杂程度,一般将数据结构分为两大类型:线性结构与非线性结构。
如果一个非空的数据结构满足下列两个条件:
① 有且只有一个根结点;
② 每一个结点最多有一个前件,也最多有一个后件。
则称该数据结构为线性结构。线性结构又称线性表。
由此可以看出,在线性结构中,各数据元素之间的前后件关系是很简单的。如例 1.5 中的一年四季这个数据结构,以及例 1.7 中的 n 维向量数据结构,它们都属于线性结构。
特别需要说明的是,在一个线性结构中插入或删除任何一个结点后还应该是线性结构。根据这一点,如果一个数据结构满足上述两个条件,但当在此数据结构中插入或删除任何一个结点后就不满足这两个条件了,则该数据结构不能称为线性结构。例如,图 1.5 所示的数据结构显然是满足上述条件的,但它不属于线性结构这个类型,因为如果在这个数据结构中删除结点 A 后,就不满足上述的条件( 1 )。
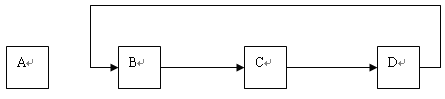
图1.5 不是线性结构的数据结构特例
如果一个数据结构不是线性结构,则称之为非线性结构。如例 1.6 中反映家庭成员间辈分关系的数据结构,以及例 1.8 中的数据结构,它们都不是线性结构,而是属于非线性结构。显然,在非线性结构中,各数据元素之间的前后件关系要比线性结构复杂,因此,对非线性结构的存储与处理比线性结构要复杂的多。
线性结构与非线性结构都可以是空的数据结构。一个空的数据结构究竟是属于线性结构还是属于非线性结构,还要根据具体情况来确定。如果对该数据结构的运算是按线性结构的规则来处理的,则属于线性结构;否则属于非线性结构。