监督分类是在图像中选择有代表性的区域作为训练区，由训练区得到各个类别的统计数据，由此建立判别函数，对整个图像进行分类。

1.判别函数
    (1)距离判别函数
欧氏距离: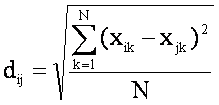

绝对值距离（出租车距离）: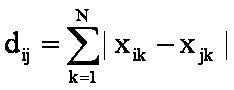

明斯基距离: 欧氏距离和绝对距离可统一表示为: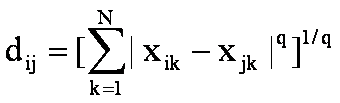

问题：1.与特征参数的量纲有关；2.没有考虑特征参数间的相关性。
    马氏距离(Mahalanobis):

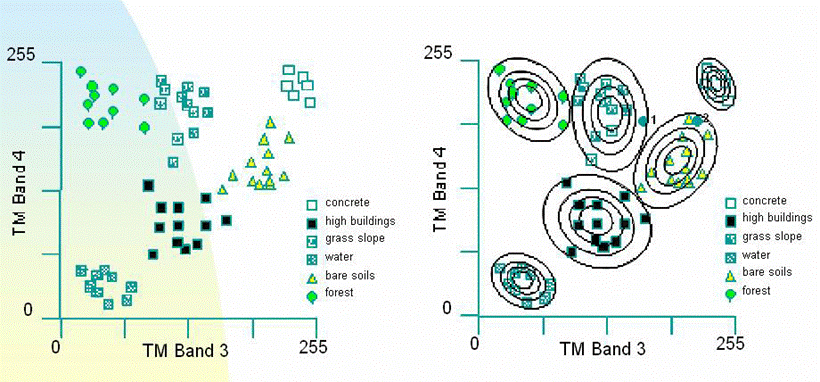
(2)最大似然法判别函数
    建立在贝叶斯准则基础上分类错误概率最小的一种非线性判别函数。
   最大似然判别规则:假设训练区光谱特征服从正态分布，计算每个像元属于每一类的概率gi(x)，找出gi(x)最大者，将该像元归为概率最大的这一类。判别函数：gi(x)=p(wi/x)。根据贝叶斯公式： gi(x)=p(wi/x)= p(x / wi)p(wi)/p(x)，p(wi/x)为x 属于wi 的概率，也称后验概率；p(x / wi)为似然概率，表示在wi这一类中出现像元X的概率， p(X)为变量x与类别无关情况下的出现概率。p(wi)为各类别的先验概率。其中:P(X/ i ): X属于i类的概率；N为参加分类的特征数(波段数)；Mi为均值向量，i为类别i的协方差矩阵；ni是类i的像元数目；j为像元标号；T矩阵的转置。
   注意：
    （1）各类别的训练数据至少要为特征维数的2到3倍以上，这样才能测定具有较高精度的均值及方差、协方差；如果2个以上的波段相关性强，则方差协方差矩阵的逆矩阵可能不存在，或非常不稳定，在训练样本几乎都取相同值的均质性数据组时，也会出现这种情况。此时，最好采用主成分变换，把维数压缩成仅剩下相互独立的波段，然后再求方差协方差矩阵。
    （2）当各类别的方差、协方差矩阵相等时，归属概率变为线形判别函数；如果类别的先验概率也相同，此时是根据欧氏距离建立的线性判别函数，特别当协方差矩阵取为单位矩阵时，最大似然判别函数退化为采用欧氏距离建立的最小距离判别法。

2.训练区的选择
（1）具有典型性和代表性
（2）所有图件时间和空间上一致性

3.最小距离分类
    一种相对简化了的分类方法。前提是假设图象中各类地物光谱信息呈多元正态分布。假设N维空间存在M个类别，某一像元距哪类距离最小，则判归该类。通过训练样本事先确定类别数、类别中心，然后进行分类。分类的精度取决与训练样本的准确与否。

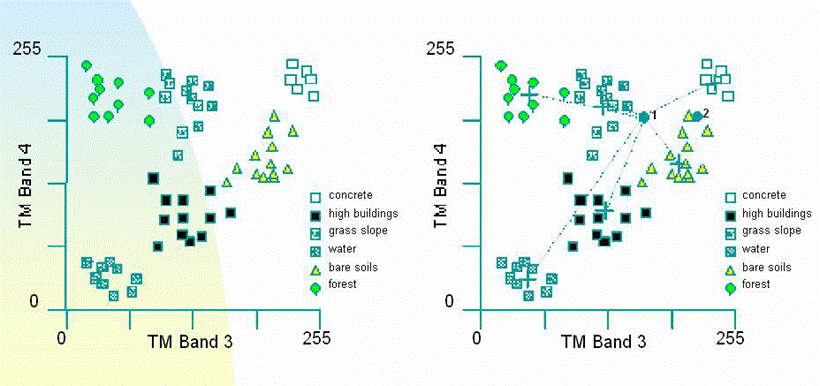
4.线性判别分类
    在多波段遥感数据形成的多维特征空间里，通过降维方法简化分类过程，并且通过投影变换把多维空间不易区分的目标转到低维空间，然后应用投影排序区分它们，从而提高可分性。用训练区像元数据通过解线性方程组方法计算出判别函数。

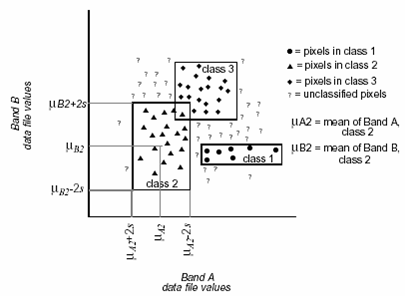
5.平行多面体分类
    使用简单的分类规则进行多光谱遥感图像的分类。决策线在n维光谱空间中是一个平行的管道，管道的直径根据距离平均值的标准差确定，如果某个像元落在某一类的平行管道的阈值范围内，则划分到该类别中；如果落在多个类中，则将这个像元划分到最后匹配的类别；落不到任何管道中，则标识为未分类像元。输入参数 Max stdev from the mean是距离平均值多少个标准差。

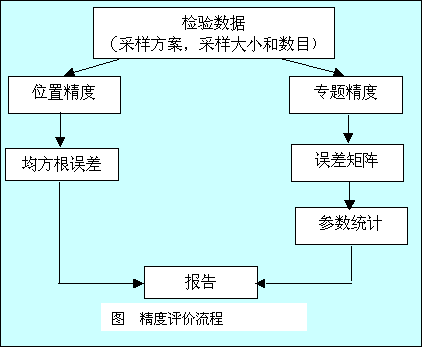
7.分类精度检验
(1)采样方法
   简单随机采样；分层采样；聚点或集群采样
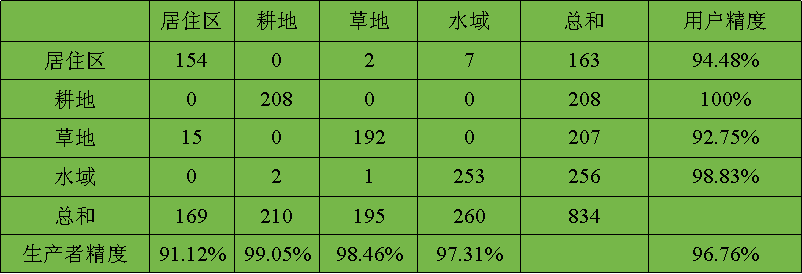
（2）误差矩阵与精度指标
    通过检验区，建立分类混淆矩阵。
    用户精度：从分类结果中任取一个随机样本，其所具有的类型与地面实际类型相同的条件概率。（错分误差）
    生产者精度（制图精度）：相对于地面获得的实际资料中的任意一个随机样本，分类图上同一地点的分类结果与其相一致的条件概率。（漏分误差）

(3)Kappa系数
    Kappa Coefficient:The Kappa coefficient expresses the proportionate reduction in error generated by a classification process compared with the error of a completely random classification. For example, a value of 0.82 implies that the classification process is avoiding 82 percent of the errors that a completely random classification generates ( Congalton, 1991).