1.图像的空间域平滑

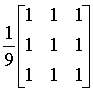
    任何一幅原始图像，在其获取和传输等过程中，会受到各种噪声的干扰，使图像恶化，质量下降，图像模糊，特征淹没，对图像分析不利。为了抑制噪声改善图像质量所进行的处理称图像平滑或去噪。它可以在空间域和频率域中进行.本节介绍空间域的几种平滑法。
（1）局部平滑法
    局部平滑法是一种直接在空间域上进行平滑处理的技术。假设图像是由许多灰度恒定的小块组成，相邻像素间存在很高的空间相关性，而噪声则是统计独立的。因此，可用像素邻域内各像素的灰度平均值代替该像素原来的灰度值， 实现图像的平滑。
   设有一幅N×N的图像f(x,y)，若采用邻域平均法所得的平滑图像为g(x,y) ,则

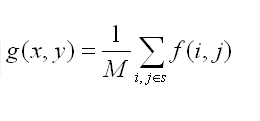
式中x,y=0,1,…,N-1;s为(x,y)邻域中像素坐标的集合,其中不包括(x,y) ；M表示集合s内像素的总数。可见邻域平均法就是将当前像素邻域内各像素的灰度平均值作为其输出值的去噪方法。例如，对图像采用3×3的邻域平均法，对于像素（m,n)，其邻域像素如下：

则有：

Z={-1，0，1}

  即：

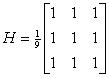
 其作用相当于用这样的模板同图像卷积。
    设图像中的噪声是随机不相关的加性噪声,窗口内各点噪声是独立同分布的，经过上述平滑后，信号与噪声的方差比可望提高M倍。这种算法简单，但它的主要缺点是在降低噪声的同时使图像产生模糊，特别在边缘和细节处。而且邻域越大，在去噪能力增强的同时模糊程度越严重。如下图：

(a)原图像，(b) 对(a)加椒盐噪声的图像，(c)3×3邻域平滑，(d) 5×5邻域平滑
   为克服简单局部平均法的弊病，目前已提出许多保边缘、细节的局部平滑算法。它们的出发点都集中在如何选择邻域的大小、形状和方向、参加平均的点数以及邻域各点的权重系数等，下面简要介绍几种算法。 （2）超限像素平滑法
    对邻域平均法稍加改进，可导出超限像素平滑法。它是将f(x,y)和邻域平均g(x,y)差的绝对值与选定的阈值进行比较，根据比较结果决定点（x,y）的最后灰度g′(x,y)。其表达式为

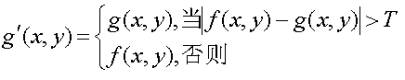
这算法对抑制椒盐噪声比较有效，对保护仅有微小灰度差的细节及纹理也有效。可见随着邻域增大，去噪能力增强，但模糊程度也大。同局部平滑法相比，超限像元平滑法去椒盐噪声效果更好。

(a)原图像，(b)对(a)加椒盐噪声的图像，(c)3×3邻域平滑，(d) 5×5邻域平滑，(e)3×3超限像素平滑(T=64)，(f)5×5超限像素平滑(T=48)
（3）灰度最相近的K个邻点平均法
    该算法的出发点是：在n×n的窗口内，属于同一集合体的像素，它们的灰度值将高度相关。因此，可用窗口内与中心像素的灰度最接近的K个邻像素的平均灰度来代替窗口中心像素的灰度值。这就是灰度最相近的K个邻点平均法。较小的K值使噪声方差下降较小，但保持细节效果较好；而较大的K值平滑噪声较好，但会使图像边缘模糊。实验证明，对于3×3的窗口，取K=6为宜。
（4）最大均匀性平滑
    为避免消除噪声引起边缘模糊，该算法先找出环绕图像中每像素的最均匀区域，然后用这区域的灰度均值代替该像素原来的灰度值。

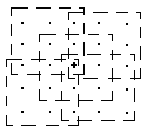
（5）有选择保边缘平滑法
    该方法对图像上任一像素(x,y)的5×5邻域，采用9个掩模，其中包括一个3×3正方形、4个五边形和4个六边形。计算各个掩模的均值和方差，对方差进行排序，最小方差所对应的掩模区的灰度均值就是像素（x,y) 的输出值。

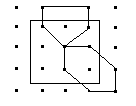
该方法以方差作为各个区域灰度均匀性的测度。若区域含有尖锐的边缘，它的灰度方差必定很大，而不含边缘或灰度均匀的区域，它的方差就小，那么最小方差所对应的区域就是灰度最均匀区域。因此有选择保边缘平滑法既能够消除噪声，又不破坏区域边界的细节。另外，五边形和六边形在（x,y）处都有锐角，这样，即使像素（x,y）位于一个复杂形状区域的锐角处，也能找到均匀的区域。从而在平滑时既不会使尖锐边缘模糊，也不会破坏边缘形状。例如，某像素5×5邻域的灰度分布如图4.2.4，经计算9个掩模区的均值和方 差为:

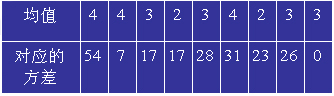
最小方差为0，对应的灰度均值3，采用有选择保边缘平滑，该像素的输出值为3。
（6）空间低通滤波法
    邻域平均法可看作一个掩模作用于图像f(x,y)的低通空间滤波，掩模就是一个滤波器，它的响应为H(r,s)，于是滤波输出的数字图像g(x,y)用离散卷积表示为

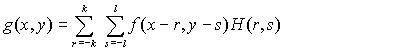
常用的掩模有:

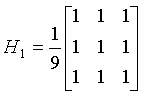
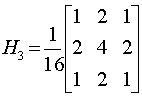
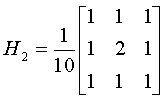
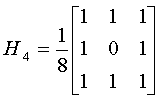
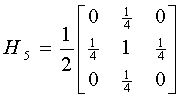
掩模不同，中心点或邻域的重要程度也不相同，因此，应根据问题的需要选取合适的掩模。但不管什么样的掩模，必须保证全部权系数之和为单位值，这样可保证输出图像灰度值在许可范围内，不会产生“溢出”现象。
（8）中值滤波
    中值滤波是对一个滑动窗口内的诸像素灰度值排序，用中值代替窗口中心像素的原来灰度值，因此它是一种非线性的图像平滑法。例：采用1×3窗口进行中值滤波，
原图像为：2 2 6 2 1 2 4 4 4 2 4，处理后为：2 2 2 2 2 2 4 4 4 4 4 。
    它对脉冲干扰及椒盐噪声的抑制效果好，在抑制随机噪声的同时能有效保护边缘少受模糊。但它对点、线等细节较多的图像却不太合适。
    对中值滤波法来说，正确选择窗口尺寸的大小是很重要的环节。一般很难事先确定最佳的窗口尺寸，需通过从小窗口到大窗口的中值滤波试验，再从中选取最佳的。

                                   原图像              中值滤波

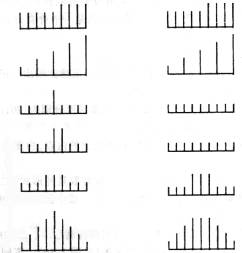
    一维中值滤波的几个例子（N=5）： 离散阶跃信号、斜升信号没有受到影响。离散三角信号的顶部则变平了。对 于离散的脉冲信号，当其连续出现的次数小于窗口尺寸的一半时，将被抑制掉，否则将不受影响。
    一维中值滤波的概念很容易推广到二维。一般来说，二维中值滤波器比一维滤波器更能抑制噪声。二维中值滤波器的窗口形状可以有多种，如线状、方形、十字形、圆形、菱形等（见图）。

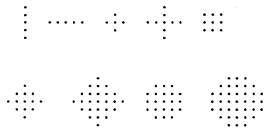
    不同形状的窗口产生不同的滤波效果，使用中必须根据图像的内容和不同的要求加以选择。从以往的经验看，方形或圆形窗口适宜于外轮廓线较长的物体图像，而十字形窗口对有尖顶角状的图像效果好。

  图(a)为原图像；图(b)为加椒盐噪声的图像；图(c)和图 (d)分别为3×3、5×5模板进行中值滤波的结果。可见中值滤波法能有效削弱椒盐噪声，且比邻域、超限像素平均法更有效。

2.图像空间域锐化

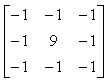
    在图像的识别中常需要突出边缘和轮廓信息。图像锐化就是增强图像的边缘或轮廓。图像平滑通过积分过程使得图像边缘模糊，那么图像锐化通过微分而使图像边缘突出、清晰。
(1)梯度锐化法
    图像锐化法最常用的是梯度法.对于图像f(x，y),在(x，y)处的梯度定义为

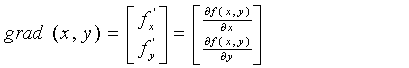
梯度是一个矢量，其大小和方向为

 对于离散图像处理而言，常用到梯度的大小，因此把梯度的大小习惯称为“梯度”。并且一阶偏导数采用一阶差分近似表示，即 :fx’ =f(x +1 ，y)-f(x，y) ，
fy’=f(x，y +1)-f(x，y)。为简化梯度的计算，经常使用grad(x，y)=Max(|fx′|，|fy′|)或 grad（x，y）=|fx’|+|f y′|。除梯度算子以外，还可采用Roberts、Prewitt和Sobel 算子计算梯度，来增强边缘。
    Roberts对应的模板如图所示。差分计算式如下：fx’ =|f(x+1,y+1)-f(x,y)| ，fy’ =|f(x+1,y)-f(x,y+1)|

    为在锐化边缘的同时减少噪声的影响，Prewitt从加大边缘增强算子的模板大小出发，由2x2扩大到3x3来计算差分，如图(a)所示。

     Sobel在Prewitt算子的基础上，对4-邻域采用带权的方法计算差分。根据梯度计算式就可以计算Roberts、Prewitt和Sobel梯度.一旦梯度算出后，就可根据不同的需要生成不同的梯度增强图像。第一种输出形式:g(x,y)=grad(x,y)，此法的缺点是增强的图像仅显示灰度变化比较徒的边缘轮廓，而灰度变化比较平缓或均匀的区域则呈黑色。第二种输出形式:

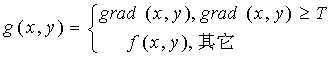
式中T是一个非负的阈值。适当选取T，可使明显的边缘轮廓得到突出，又不会破坏原来灰度变化比较平缓的背景。第三种输出形式:

此方法将背景用一个固定的灰度级 LB来表现，便于研究边缘灰度的变化。第五种输出形式:

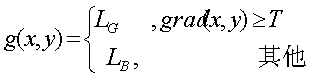
这种方法将明显边缘和背景分别用灰度级LG和LB表示，生成二值图像，便于研究边缘所在位置。

(2)Laplacian增强算子
    Laplacian 算子是线性二阶微分算子。即▽2f(x，y)=

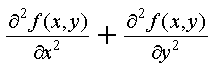
对离散的数字图像而言,二阶偏导数可用二阶差分近似，可推导出Laplacian算子表达式为▽2f(x，y)= f(x+1，y)+f(x-1，y)+f(x，y+1)+f(x，y-1)-4f(x，y)。Laplacian增强算子为：g(x，y)=f(x，y)- ▽2f(x，y)=5f(x，y)-[ f(x+1，y)+ f(x-1，y)+f(x，y+1)+ f(x，y-1)]

 其特点是：在灰度均匀的区域或斜坡中间▽2f(x,y)为0,增强图像上像元灰度不变；在斜坡底或低灰度侧形成"下冲" 而在斜坡顶或高灰度侧形成"上冲"。
(3)高通滤波法
   高通滤波法就是用高通滤波算子和图像卷积来增强边缘。