对多光谱图像进行线性变换,减少各波段信息之间的冗余,达到保留主要信息,压缩数据量,增强和提取更有目视解译效果的新波段数据的目的。设f为数字图像f(x,y)的灰度值方阵,大小为NN,显然f是实数矩阵。实数矩阵总可以经过一系列初等变换,找到它的同型矩阵F,使得:F=PfQ,式中F、f是NN方阵, P、Q是NN的满秩方阵,且P、Q不唯一。由于P、Q满秩,它们有逆矩阵P-1、Q-1,分别用P-1左乘,右乘Q-1上式,f=P-1FQ-1。表明:数字图像可以从它的正交变换中完整地恢复。
1.K-L变换(1)原理
在遥感图像处理中又称作主成分分析(PCA,Principal Component Analysis)。遥感多光谱影像波段多,一些波段的遥感数据之间有不同程度的相关性(光谱反射的相关性、地形、遥感器波段间的重叠),造成了数据冗余。K-L变换的作用就是保留主要信息,降低数据量,从而达到增强或提取某些有用的信息的目的。
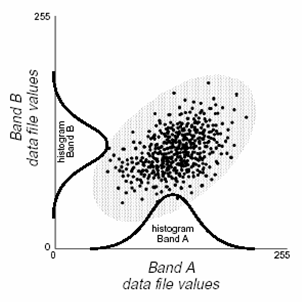
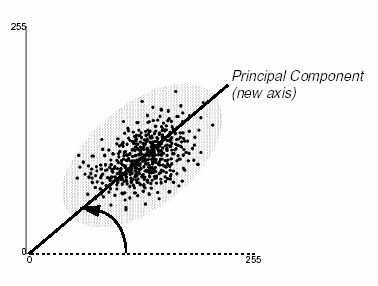
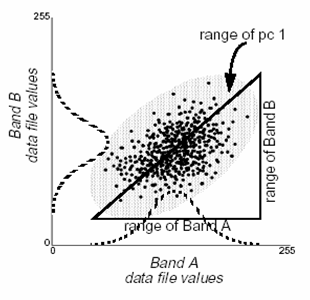
从几何意义来看,变换后的主分量空间坐标系与变换前的多光谱空间坐标系相比,旋转了一个角度,而且新的坐标系的坐标轴一定指向数据信息量较大的方向。以二维空间为例,假定某图像像元的分布为椭圆状,那么经过旋转后新坐标系的坐标轴一定分别沿椭圆的长半轴和短半轴方向――主分量,因为长半轴这一方向信息量最大。 基于上述特点,在遥感数据处理时常常用K-L变换作数据分析前的预处理,可以实现数据压缩和图像增强的效果。在遥感图像分类中,常常利用主成分分析算法来消除特征向量中各特征之间的相关性,并进行特征选择。
(2)方法
求出一个变换矩阵,经变换形成一组新的主分量波段,公式为:Y=AX,其中,Y为变换后的主分量矢量,如主分量1,2,3…,X为变换前的原始图像矢量,如TM1,TM2,…, A为变换矩阵。
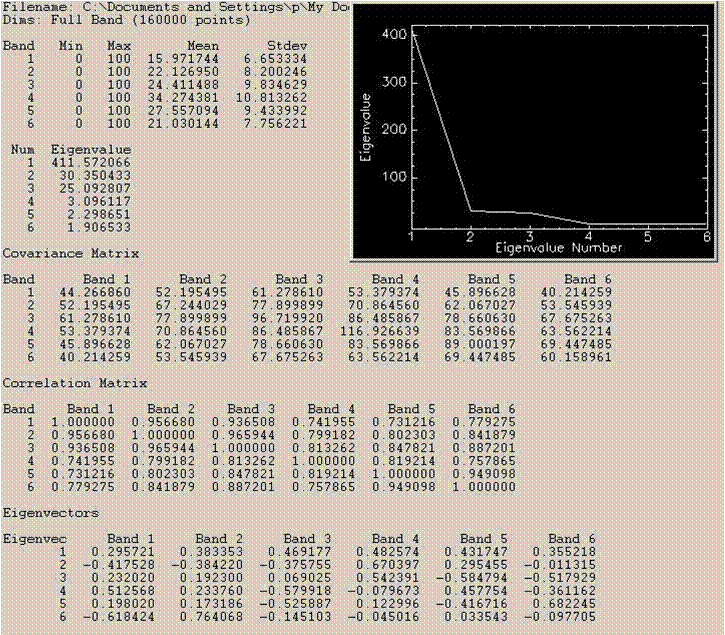
步骤:计算原始图像的方差-协方差矩阵;计算特征值和特征向量;生成主成分。
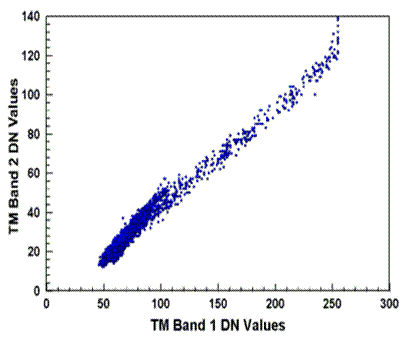

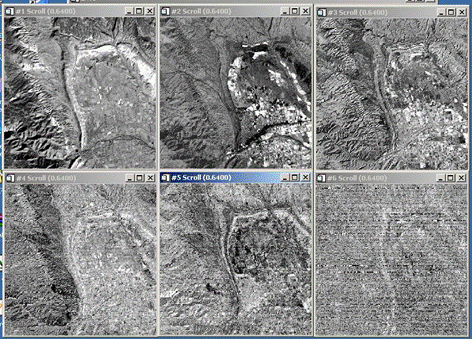
原始图像TM1-5,7 主成分图像PC1-6

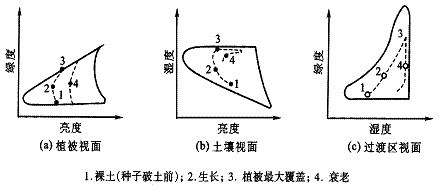
K-T变换又称缨帽变换。1976年,Kauth和Thomas发现了一种线性变换,它使坐标空间发生旋转,但旋转后的坐标轴不是指向主成分的方向,而是指向另外的方向,这些方向与地面景物有密切的关系,特别是与植物生长过程和土壤有关。这种变换既可以实现信息压缩,又可以帮助解译分析农业特征,因此有很大的实际应用意义。缨帽变换也是一种线性变换,它也遵循一般线性变换的形式。目前对这个变换的研究主要集中在MSS与TM两种遥感数据的应用分析方面。TM数据K-T变换后的景观意义可通过下图形象说明,图中1、2、3、4分别代表作物从发芽到枯黄生长的不同阶段。绿度与亮度组成的二维空间称植被视面,它反映了植被从破土发芽到生长旺盛阶段随叶面积增加而绿度值增加,之后开始成熟枯黄,绿度也逐渐降到最低点。湿度与亮度组成的平面为土壤视面,绿度与湿度组成的平面称过渡区视面,都不同程度地反映了作物生长过程中植被与土壤的变化信息。
K-T变换同样是通过一变换矩阵来实现的:Y = AX
以TM数据为例,Crist和Cicone计算出新的变换矩阵如下:
0.3037 0.2793 0.4743 0.5585 0.5082 0.1863
-0.2843 -0.2435 -0.5436 0.7243 0.0840 -0.1800
A = 0.1509 0.1973 0.3273 0.3406 -0.7112 -0.4573
-0.8242 -0.0849 0.4392 -0.0580 0.2012 -0.2768
-0.3280 -0.0549 0.1075 0.1855 -0.4357 0.8085
变换后得出六个新的分量,前三个分别称为:Y1亮度,Y2绿度,Y3湿度,后三个分量没发现特定指示意义。这样TM 1、2、3、4、5、7六个波段数据经过K-T变换提取出有特定含义的三个分量,这在植被和土壤分类以及作物估产研究中都有重要作用。TM 数据K-T变换后的景观意义可通过图形象说明,图中1、2、3、4分别代表作物从发芽到枯黄生长的不同阶段。绿度与亮度组成的二维空间称植被视面,它反映了植被从破土发芽到生长旺盛阶段随叶面积增加而绿度值增加,之后开始成熟枯黄,绿度也逐渐降到最低点。湿度与亮度组成的平面为土壤视面,绿度与湿度组成的平面称过渡区视面,都不同程度地反映了作物生长过程中植被与土壤的变化信息。