1.中心投影构像（航片）的几何纠正
    目的：将中心投影影像纠正成正射投影影像。      
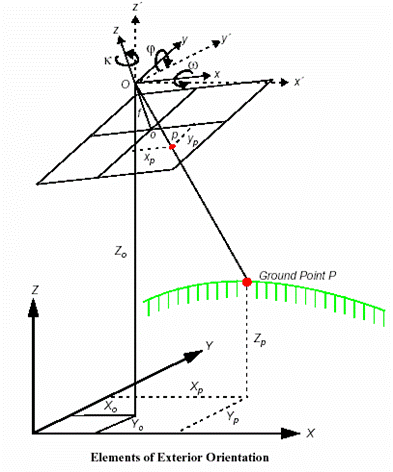
    航片的成像特点：
（1）地物通过摄影中心与其成像点共一条直线；
（2）投影中心到像平面的距离为物镜主距f；
（3）地面起伏使得各处影像比例尺不同；
（4）地物由于成像平面倾斜其成像会发生形变；
（5）具有高差的物体成像在相片上有投影差。
    将中心投影影像纠正到正射投影影像时必须考虑到地面的高程信息：①利用已知DEM；②建立立体模型，利用左右视差解算出地面高程。

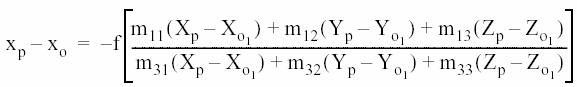
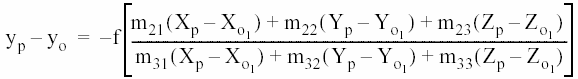
2.航片的立体模型
    航空摄影中需要在同一照相高度，从两个不同角度对同一地区拍摄的两张像片（一个立体像对）才能构成立体模型。同一物体在两张空中照片上，呈现出互有差别的影像，并具有不同的左右视差，假若用两眼代替镜头，分别各看一张照片，则各像点在眼睛网膜上所形成的影像，同样会形成不同的生理视差而获得物体的立体效应。

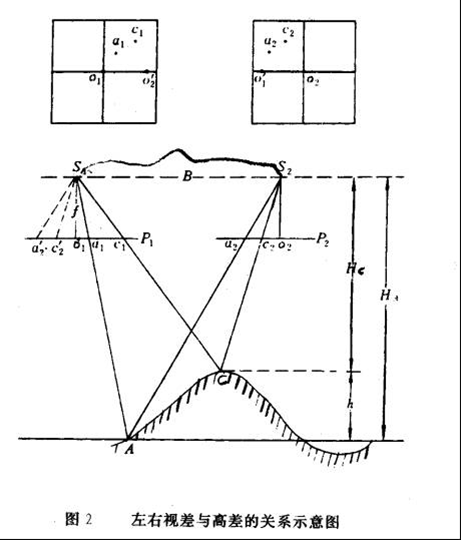
    像对上同名地物点的横坐标差称为左右视差（横坐标差），如图所示，地面点A在左右两像片上的影像分别为a1 、a2，A点在左像片上的横坐标为Xa1，在右像片上的横坐标为Xa2，A点左右视差Pa= a1 +a2。同样，C点的左右视差Pc= c1 +c2。地面上A C两点的高差 h = Ha–Hc（以A为基准点），S1 S2为摄影基线实长，Pa= a1 +a2和Pc= c1 +c2 ，表示A点和C点的左右视差。根据它们的几何关系（图中ΔS1a’2a2与ΔS2A S1），用相似三角形对应边的比可推导得到高差与左右视差的关系公式，即：h = Δp.HA /(b+Δp),式中：h为C点相对基准点A的高（程）差；Δp为A、C两像点间的左右视差较（PC-Pa）,即C像点的左右视差相对A像点的左右视差的差数。b为像片上摄影基线长（同一航片上两个像主点距离），HA为航高。

3.多中心投影影像的构像方程
（1)CCD推帚式传感器

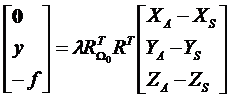
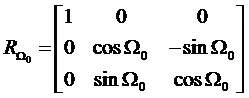
（2）全景摄影机

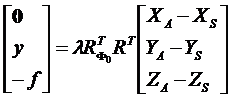
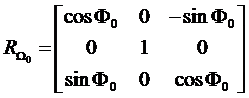
(3)红外和多光谱扫描仪

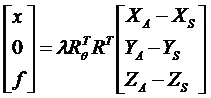
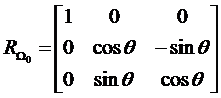
4.多中心投影构像的简易几何校正方法
有多项式方法、随机场内插方法等等，其中多项式方法的应用最为普遍。 共线方程方法虽然方法严密又比较精确，但由于计算比较复杂，且需要控制点高程数据，故应用受到限制。

    该法的基本思想是回避成像的空间几何过程，而直接对图像变形的本身进行数学模拟。它把遥感图像的总体变形看作是平移、缩放、旋转、仿射、偏扭、弯曲以及更高次的基本变形的综合作用结果，因而纠正前后图像相应点之间的坐标关系可以用一适当的多项式来表达。常用的二元齐次多项式纠正变换公式可表达为：
x=a0+（a1X+a2Y）+（a3X2+a4XY+a5Y2）+（a6X3+ a7X2Y + a8XY2+a9Y3），y=b0+（b1X+b2Y）+（b3X2+b4XY+b5Y2）+（b6X3+ b7X2Y + b8XY2+b9Y3），式中：x、y为某像元的原始图像坐标， X、Y为纠正后同名点的地面（或地图）坐标，ai、bi为多项式系数（i=0、1、2、3、4）。