1.几何校正的原理
    遥感图象的几何粗处理和精处理。一般地面站提供的遥感图像数据都经过几何粗校正，因此这里主要介绍一种通用的精校正方法。
    遥感图像的几何纠正按照处理方式分为光学纠正和数字纠正。
    遥感图像的几何纠正就是将含有畸变的图像纳入到某种地图投影。对地面覆盖范围不大的单幅图像，一般以正射投影方式使其改正到地球切平面上。
    光学纠正主要用于早期的遥感图像的处理中，现在的应用已经不多。除了对框幅式的航空照片（中心投影）可以进行比较严密的纠正以外，对于大多数动态获得的遥感影像只能进行近似的纠正。主要介绍数字图像的几何纠正，能够较精确地改正线性和非线性变形误差。

2.什么情况下需要做精纠正？
（1）景与景间的比较，如变化监测；
（2）为GIS建模开发数据库；
（3）分类前按照地图坐标进行训练样本的选取；
（4）创建带有精确比例尺的影像地图；
（5）矢量数据与影像的叠加；
（6）不同比例尺图像间的比较；
（7）提取精确距离和量算面积；
（8）图像镶嵌。

 3.多项式法数字图像纠正的处理过程

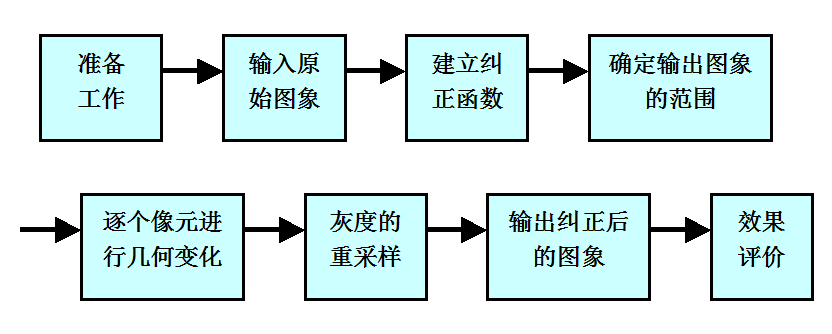
     两个基本环节：像元坐标变换和像元灰度值重采样。
     (1)确定输入图像和输出图像的坐标变换关系
数字图象几何纠正：通过计算机对离散结构的数字图像中的每一个像元逐个进行纠正处理的方法。这种方法能够精确地改正动态扫描图像所具备的各种误差。
基本原理：利用图像坐标和地面坐标（另一图像坐标、地图坐标等）之间的数学关系，即输入图像和输出图像间的坐标转换关系实现几何校正。
直接纠正方法:从原始图像阵列出发，按行列的顺序依次对每个原始图像像元点位用变换函数 F（）（正解变换公式）求得它在新图像中的位置，并将该像元灰度值移置到新图像的对应位置上。
间接纠正法:从空白的新图像阵列出发，按行列的顺序依次对新图像中每个像元点位用变换函数f () （反解变换公式） 凡求其它在原始图像中的位置，然后把算得的原始图像点位上的灰度值赋予空白新图像相应的像元。

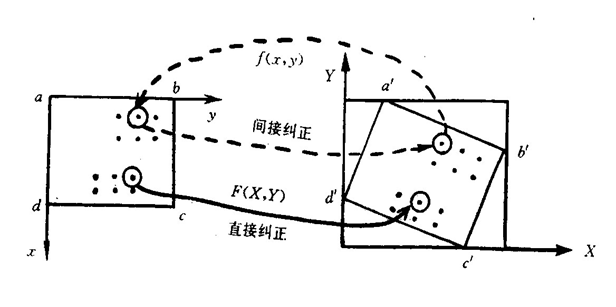
    (2)确定新的图像的边界
纠正后图像和原始图像的形状、大小、方向都不一样。所以在纠正过程的实施之前，必须首先确定新图像的大小范围。

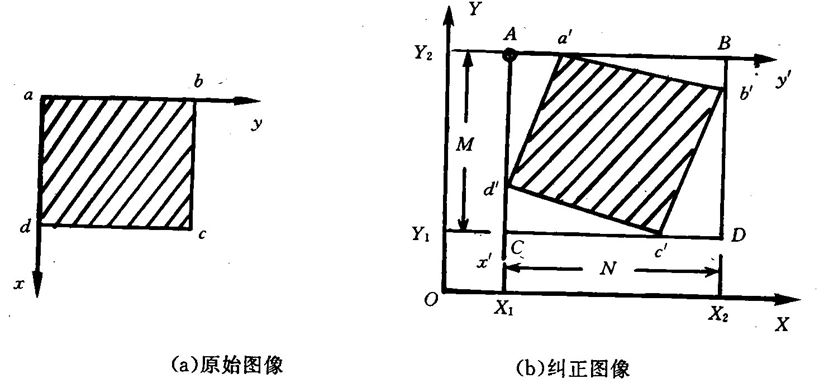
根据正解变换公式求出原始图像四个角点（a, b, c, d）在纠正后图像中的对应点（a’, b’, c’, d’）的坐标（Xa’,Ya’）(Xb’,Yb’) (Xc’,Yc’) (Xd’,Yd’)，然后求出最大值和最小值。X1 = min (Xa’, Xb’,  Xc’, Xd’)，X2 = max (Xa’, Xb’, Xc’, Xd’)，Y1 = min (Ya’, Yb’, Yc’, YXd’)，Y2 = max (Ya’, Yb’,Yc’, Yd’)。
    (3)确定新图像的分辨率
     目的是把边界范围转换为计算机中纠正后图像的储存数组空间。必须在新图像的范围内，划分网格，每个网格点就是一个像元。根据精度要求，定义输出像元的地面尺寸ΔX,ΔY，并以边界范围左上角A点为输出图像的坐标原点。x’轴（AC）表示图像行号,y’(AB)表示图像列号。新图像的行数 M＝(Y2-Y1)/△Y+1;新图像的列数 N＝(X2-X1)/△X+1;新图像在A- x’ y’坐标系的任意一个像元的坐标由它的行列号唯一确定。行列号范围： x’ =1，2，┅ ，M；y’ =1，2，┅ ，N。
    (4)灰度的重采样
    纠正后的新图像的每一个像元，根据变换函数，可以得到它在原始图像上的位置。如果求得的位置为整数，则该位置处的像元灰度就是新图像的灰度值。如果位置不为整数，则像元灰度值需根据周围阵列像元的灰度确定，这种方法称为灰度重采样（这是相对遥感图像获取时已进行过一次采样而言）。常用的方法： 1)最近邻法，2)双线性内插法，3）三次卷积法。

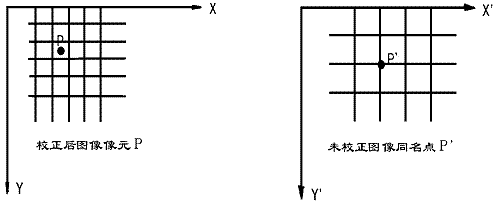
1) 最近邻法：距离实际位置最近的像元的灰度值作为输出图像像元的灰度值；

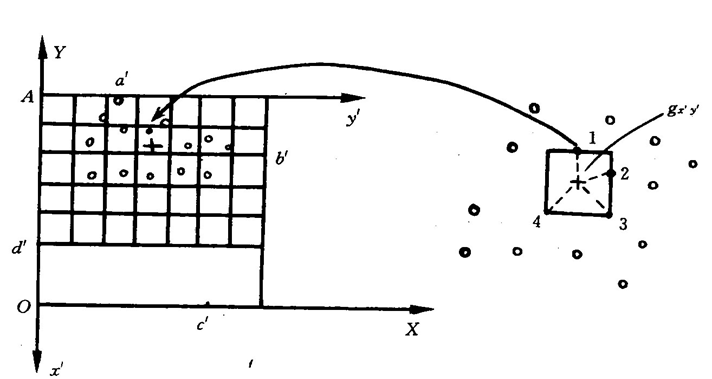
2）双线性法：以实际位置临近的4个像元值，确定输出像元的灰度值。公式为：

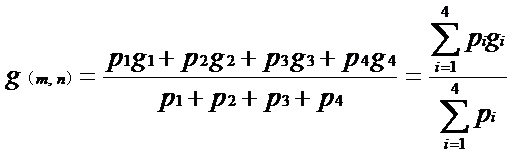
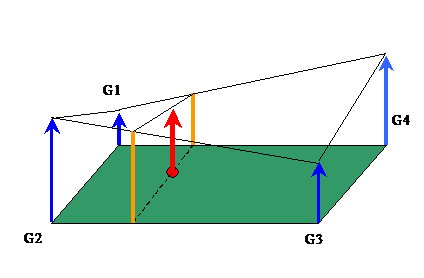
3）三次卷积法以实际位置临近的16个像元值，确定输出像元的灰度值。公式为：

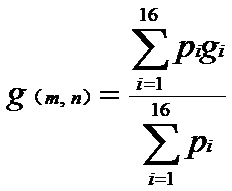
4.