流体流动与输送

流体的最大特点是：其质点几乎有无限的流动性，且几乎可以毫无阻力地将其形状分裂或改变。流体：液体——不可压缩

                               气体——可压缩

在这里把压缩性视为气体与液体的主要区别点。

§2-1 一些基本概念

2-1.1 理想流体和实际流体

把流体视为由无数个流体微团（或流体质点）所组成，这些流体微团紧密接触，彼此没有间隙。这就是连续介质模型。

流体微团（或流体质点）：宏观上足够小，以致于可以将其看成一个几何上没有维度的点；同时微观上足够大，它里面包含着许许多多的分子，其行为已经表现出大量分子的统计学性质。

理想流体    指不具有粘度，流动时不产生摩擦阻力的流体。 

理想液体    不具有粘度的液体，流动时不产生摩擦阻力的液体。具有不可压缩、受热不膨胀的性质。 

理想气体    不具有粘度的气体，流动时不产生摩擦阻力的气体。服从理想气体状态方程

理想气体状态方程

以当时条件与标准条件对比时

2-1.2 流体的密度、相对密度和比容

1、密度  单位体积流体所具有的质量。用表示  

  [kg/m3]          （1）

气体混合物的密度

气体具有压缩性，它的密度随压强和温度的不同差别很大。在温度不太高、压力不太大时，气体的密度可近似地用理想气体状态方程式来处理。对于单一组分来说，

PV=nRT=

             （2）

标准状态：T0 =273 K，P0=101.3 kPa，V0=22.4 m3/kmol

则 （n=1） 代入上式

         （3）

（3）式比（2）式用起来更为方便，且不易出差错。

若为气体混合物，其密度可按平均分子量求算，因为气体中组分的含量为体积百分数，也就是mol %。

平均分子量  Mm=M1x1+M2x2 + …  代入（3）得,

             （4）

2、相对密度  是指给定条件下某一物质的密度r1与另一参考物质的密度r2之比。

3、比容  单位质量流体所具有的体积

                （5）

比容与密度互为倒数，它多用于气体。

2-1.3 流体的压力及其测量

一、流体的压力

1、压力

液体垂直作用在单位面积上的力称为压力（也称为压强）。

2、压力的单位  表示压力的单位很多：

在SI制中，压强的单位是N/m2，称为Pa。

N=kgm/s2，

在物理学（cgs）中，压力的单位可以用：大气压、mmHg、mH2O等。

工程单位制中，用kgf/cm2 。

它们之间的关系

1绝对大气压=101.325kPa=760mmHg=10.33mH2O=1.033kgf/cm2

1工程大气压=100kPa=735.6mmHg=10mH2O=1kgf/cm2

以液柱表示的压力

[Pa]

也可写成  [米液柱]         （6）

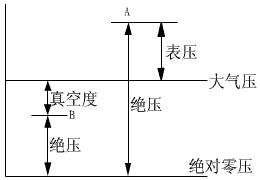
3、压力的基准

A、绝对压强

凡是用绝对0压（即绝对真空）作为起点计算的压强，称为绝对压强。

B、表压

体系的压强比大气压高出的部分称为表压。              

体系内：  绝对压=大气压+表压          

表压=绝对压 - 大气压

C.真空度

体系的压强低于大气压的部分

体系内：  绝对压=大气压 - 真空度

          真空度=大气压 - 绝对压

真空度是表压强的负值。

D、三者之间的关系

二、流体静力学基本方程式

静止流体内部静压强的特点：

（1）、静止流体内部任意一点各个方向作用于它的压强相等。

（2）、静止流体内部同一水平面上，各点静压强相等。

1、基本方程式的推导

基准面取容器的底面

液柱截面积=A

向上作用的浮力= f2

向下作用的力= f1

液柱本身的质量：

液柱本身的重力：

平衡时    ，  两边除以底面积A

 ，

  [m液柱]           （7）

上式即为流体静力学基本方程式。

它表示了：在静止流体内部任意一水平面上压强的大小。

2、基本方程式的使用条件

（1）、静止的、连通的、同种流体的内部。

（2）、也适用于气体。（虽然用液体导出）

气体可压缩，随位置而变，但化工容器体积有限，的变化可忽略，故对于气体也适用。

在同一水平面上，且连通的、静止的、同种流体的内部。

∴，

虽在同一水平面，又是连通的同种流体，但不是连通而又静止的同一流体，∴，

（3）、处于相对静止的流体也适用，水槽的截面积远大于吸水管的截面，

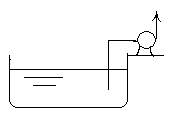
槽内液位下降速度很小，可忽略，故槽内液体叫做相对静止。

三、基本方程式的应用举例

1、U型管压差计

对指示液A的要求  与被测流体不互溶

             >

 ，  ，

整理得         （8）>

若被测流体为气体，则>> ， 可忽略，上式可变为，

 对（8）式进行讨论，

a、若P1—P2一定，（即两端压差一定）

在一般情况下，尽量使h保持一定的高度，这样读取数据时误差小，且方便。

B、若   希望   

     希望    

c、通过（7）式的推导，可以看出

                       与U的粗细无关

U型管两端的压差显示      与m的长短无关。

与A、B两流体的密度差有关。

与读数h有关。

2、微差压差计（双液液柱压差计）

若所测量的压差很小，h就小，难读精确，为放大h数值，除选用、非常接近外，另一办法就是选用微差压差计。

>>

                (9)       

推导: 

      ，    

∴，

微差压差计主要用于测量系统两端的微小压强差。在相同的压强差时,它的读数h一般比U型管压差计放大几十倍。为了把测量误差控制在1~2%，U的直径d与扩大小室的直径D相比，要求d:D=1:10

3、液面计（液位计）

 液面计是根据静止流体在同种流体内，同一平面上各点的压强相等这一原理设计的，被测液面高度与液面计所用玻璃管的直径无关。

2-1.4 流量和流速

1．流量

流量——有体积流量与质量流量两种

   体积流量——单位时间流过导管任一截面的流体体积；qv  [m3/s]

   质量流量——单位时间流过导管任一截面的流体质量；qm  [kg/s]   

   关系   qm ＝ r·qV

2．流速

流速——流体质点于单位时间内在导管中流过的距离， 

流速  

3.管径的初选

在管径的选择中，如果选用较小的管径，可以降低基建费用，但在一定的流量条件下，管径越小，流动阻力也随之增大，能耗也将相应增大。因此，合理的管径应综合多方面的因素来确定。一般条件下，可根据选用的流速来对管径进行初步选择，再在次基础上进行多方面的评比来确定实用的管径。

                  即：

2-1.5 定态流动和非定态流动

1、定态流动  流体流动过程中，任一截面上与流动相关的物理量 (流速、压强、密度等) 不随时间变化的流动。

2、非定态流动  在流动过程中，流体在任一截面上的物理量既随位置变化又随时间而变化的流动。  

§2—2  流体定态流动时的衡算

2-2.1 流体定态流动时的物料衡算

物料衡算的依据：质量守恒定律

按照质量守恒定律的原则：

推导前提     连续流体

          稳定流动

连续流体的性质：   可无限分割，而不改变其物性

                表征流体流动的参数，可连续变化

物料衡算

1、划定衡算范围1—1’ , 2—2’

2、选基准时间1S

3、列衡算式        （质量流量）

∴，

此式即是物料衡算式，又叫连续性方程。

对于不可压缩性流体，，∴，

对于圆管，      

可见流量一定，流速    与管道横截面积成反比

与管径d2成反比。

2-2.2 流体定态流动时的能量衡算

一、柏努利方程式的建立

流体流动的必要条件是系统两端有：压强差或位差。流体流动的过程实质上是能量转化过程。流体作稳定流动时，有四种能量可能发生变化。即    位能

          动能        机械能

          静压能

          内能

能量之间是可以互相转化的，内能与机械能之间也是如此。例如，因为流体具有粘性，流动时因摩擦、碰撞，因而有一部分机械能转化为热能，使流体温度升高，变为流体的内能，这种过程只有流体流动时才较明显。

为了使问题简化，我们首先建立理想液体的柏式。

绝对不可压缩（比容不随压强P而变）

理性液体的特点    完全没有粘性（无内摩擦力，即没有机械能向内能的转化，即T不变）

流动时无阻力。

因此，理想流体流动时，只有机械能之间的转化，而无内能的增减。

对上图稳定流动系统进行能量衡算：

衡算范围：1—1’，2—2’截面之间

衡算基准面：0—0’水平面

对于稳定流动，每m kg流体经截面1—1’进入系统内，必有m kg流体经截面2—2’离开这个系统。∴，以m kg流体作为衡算的基准。

1、位能

流体受重力的作用，在不同的高度具有不同的位能。它是个相对值。

位能= mgH

单位：mgH= kg×m/s2×m = Nm =J

∴，mgH流体在截面1—1’ ，2—2’所具有的位能分别为：mgH 1 , mgH2

2、动能

流体流动时所具有的能量。

动能=

这一能量相当于将mkg流体从速度为零加速到速度为所做的功。

单位：= kg×m2/s2= Nm = J

mkg流体在截面1—1’，2—2’处所具有的动能分别为：，

3、静压能（流动功）

在静止或流动的流体内部任一处都有一定的静压强。

如在内部有液体流动的管壁上开一孔，装一垂直玻璃管，液体便会在玻璃管内上升一定高度，这个液体高度便是运动的流体在该截面处静压强的表现。对于我们的衡算系统，流体通过截面1—1’时，由于该截面处流体具有一定的压力，这就需要对截面之外的流体做相应的功，以克服这个压力，才能将流体推进系统里去。于是通过1—1’截面的流体必定要带着与所需的功相等能量进入系统，流体所具有的这种能量称为静压能或流动功。

如mkg流体，体积为V[m3]，通过截面1—1’，把该流体推进此截面所需的作用力=P1A1。

流体通过此截面所走的距离=，

流体带入系统的静压能=

单位：   

同理：2—2’截面处流体所具有的静压能为P2V2。

根据能量守恒与转化定律，两截面所具有的总机械能相等，即

两边除以m     ， V=V1=V2    

 [J/kg]              （1）

两边除以g， [米液柱]（2）

上式即为理想流体的柏努利方程式，也叫能量衡算方程，流体动力学方程。

上式中各项表示：1kg流体所具有的能量。

二、柏式的引申

在工业生产中所遇到的流体都是实际流体。实际流体有粘性，所以在流动时有摩擦阻力产生，其数值的大小视   

流体的性质        

                流动的状况

                管壁的粗糙程度      而定。

流体流动时总有一部分能量消耗在摩擦阻力上。由于克服流体阻力，消耗了一部分机械能，这部分机械能转变成了热能，而热能又不能直接用于流体的输送，只能被流体吸收，使流体温度略有升高。所以，从实用的角度来讲（或从机械能的衡算来讲），这部分机械能是损失掉了。有外加流体输送机械对流体作功。所以，实际流体的柏努利方程式变为：

   [m]     (3) 

流体输送所需功率是指：单位时间耗用的能量，

实际功率 [kW] （4）

式中：Pe－理论功率

－输送设备的效率

工程上将每kg流体所具有的各种形式的能量统称为压头，如

H：位压头（简称位头）

 ：动压头，又称速度头。

：静压头

He：输送设备对流体所提供的能量，又称有效压头。

：因阻力所消耗的能量，又称压头损失。

压头—可以互相转化，是某一截面的能量。

压头损失—为沿程的压头损失，不是某一截面的。压头一经损失掉，就不能变回系统里任何一种形式的压头。

三、柏努利的讨论

1、方程使用条件：连续系统，稳定流动，不可压缩性流体。

2、对于气体，当压强变化时，公式仍适用，其结果是足够准确的。计算时只需将气体的密度用平均密度代替，即  。

3、对于静止流体，=0，He=0，=0，则（3）式变为

此式即为流体静力学基本方程式。因此看出静力学方程是柏努利方程的一个特殊形式。

4、对于实际流体的流动，，它有压头损失。

5、对于不稳定流动，在任一瞬间柏式方程仍能成立。

四、应用柏式解题要点

（一）、画示意图，标明流动方向

（二）、选截面

取截面是为了确定能量的衡算范围。

1、需求取的未知量必须在截面上或两截面间。

2、流动方向与截面相垂直。

3、以上游为1—1’，下游为2—2’，把所选截面标在图上。

4、截面不要选在转弯处或直径突变处。

（三）选水平基准面

流体的位头是由它所处的位置距水平基准面的高度而定，在能量衡算中，须求取的是流动系统中两截面间的位头差。

1、水平基准面的的高度可以任意选取，但必须与地面平行。

2、截面位置在水平基准面的上方，其位压头为正，反之为负。

3、把所选基准面标在图上。

（四）单位要统一（SI制）

五、柏式应用举例

1、确定容器间的相对位置

已知：高位槽和反应器均为敞口容器。

管内流速=2[m/s]，Hf =2[m] ，求 h

解：在1—1’，2—2’间列柏式，以0—0’为基准面。

H1=h，H2=0，P1=P2=0（表压）

= 0， = 2[m/s] ，Hf = 2m，He = 0

∴，  [m]

2、确定管路中流体的压强

已知，kg/m3 ，=2m/S ，=8m/s

P1=1.2kgf/cm2（表压），Hf =0 （忽略），求 P2  

解：在1—1’，2—2’ 间列柏式，以0—0’为基准面。

H1=0，He=0，Hf =0

3、确定输送设备的有效功率

已知料液=1200kg/m3 ，蒸发室真空度=200mmHg，输送管道 684，体积流量=20m3/h ， ，求泵的理论功率。

解：在1—1’，2—2’间列柏式，以0—0’为基准面。

H1=0 ，  H2=15m ，P1=atm ，=0

P2=（真空度）

P2=101325-26665=74660Pa（绝对压）

  m/s

理论功率：

2-2.4 流体流量的测量              

在化工生产中，为了控制生产过程能够稳定运行，就需要经常了解温度、压强、流量等操作条件，并加以调节控制。流体的流量是生产操作中必须测量与控制的重要参数之一。流量计就是常用的测量工具。

下面介绍的几种流量计都是根据流体流动中能量转换关系而设计的流量计。

一、孔板流量计

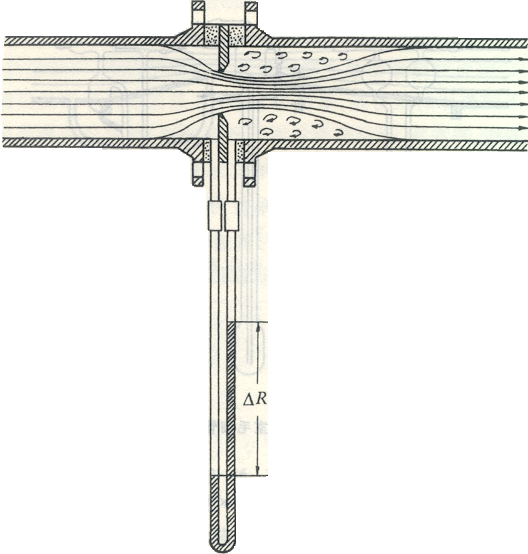
在1—1’,2—2’间列柏式，基准面取管中心线。 Hf  = 0（暂时看作）

，     （1）

——缩脉处流速

         1、未考虑Hf（它不等于0）

上式中   2、缩脉处的截面积A2是随流动条件而改变的未知（缩脉直径的大小、位置随流况而变）。∴，无法知道。

         3、孔口截面积A0为已知，∴，孔口流速也已知，用代替

                  1、不可忽略的Hf 。

用校正系数C来校正   2、缩脉截面积与孔口截面积之差。

3、上、下游测压口的位置。

用A0代替了A2， 代替了，也应该用P0代替P2，但不能把2—2’的测压口正好装在孔板上，比较常用的一种方法是把上、下游两个测压口紧靠着孔板前后的位置上，这种取压法叫角接取压法。∴，测压口的位置也应该校正。（1）变为，

                （2）

   U测压计公式： ，两边除以，

       代入（2）

   [m/s]       （3）

体积流量    

——校正系数，由实验确定，一般在0.61~0.62之间。

对于标准的孔板，有图表可查。

为了测量准确，孔板与上游管件应距 50d1 ,

                  与下游管件应距 10 d1 。

若较小，这个距离可缩短些。

孔板流量计的优点：易于制造；适合大流量的测量。

缺点：流体流经孔板的能量损失大；孔板的锐边容易腐蚀、易磨损，流量计应定期进行校正。

二、文丘里流量计

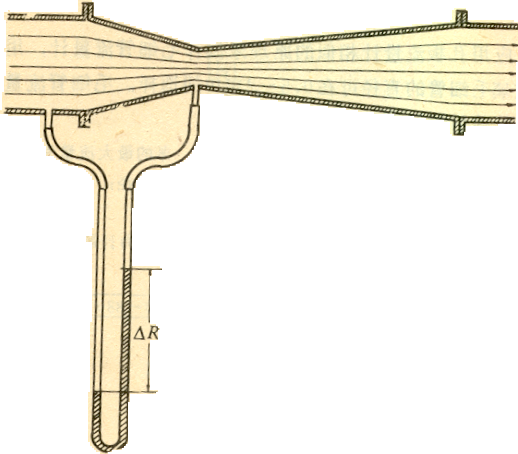
为了减少流体流经孔板的能量损失，用一支渐缩渐扩管代替孔板。这样构成的流量计称为文丘里流量计。

上游测压口处距管径开始收缩处的距离至少应为。下游测压口在喉部。由于渐缩和渐扩，流体在管内流速改变平缓，所以阻力损失小。

文丘里流量计的计算公式与孔板流量计相类似。

   [m/s]           （4）

         [m3/s]

——流量系数，无因次，其值由实验确定或从仪表手册中查得。

三、转子流量计

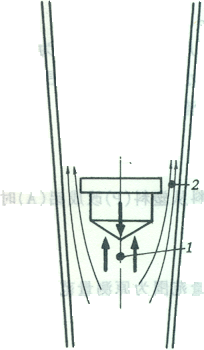
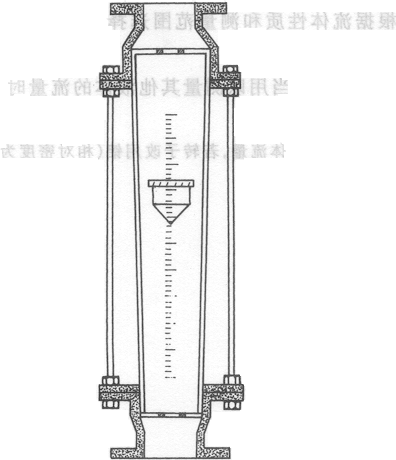
1、工作原理

当流体通过转子与玻璃管形成的环隙时，流道截面积A,流速，流体静压强，在转子上产生一个压力差，，即向上的推力,转子。

设  ——转子的体积  

——最大截面积

   ——转子的密度

若：上游环形截面为，下游环形截面为，则流体流经环形截面所产生的压强差为。

压力差（向上的推力）      转子所受重力 — 浮力＝转子净重力

 若                      >                       转子

                         <                       转子

 平衡时                  =              转子停留在某一位置

即  

                    (5)

从上式看出：、g、、、均为定值。

 ∴，也为定值，与流量无关。

当转子停留在某一位置时，转子与管间的环形截面积一定。流体通过此环形时，流速与静压强的变化关系与通过孔板流量计孔口的情况相似。因此，转子流量计的计算公式可仿照孔板流量计的公式写出。

    [m/s]       （6）

  [m3/s]

式中 ——校正系数，无因次，由实验确定或查手册。

——环隙面积，m2

转子流量计的优点：1、能直接观察到流量计内流体的流动状况。

             2、压头损失小，测量范围宽。

             3、流量计前后不需要有一定长度的直管段。

注意：安装时必须保持垂直。

孔板流量计与转子流量计的区别         

    由于转子流量计的不随而变，只改变转子所处的截面位置，所以又叫截面流量计。通过环隙压强差（P1-P2）不变，所以又叫恒压差流量计。

2、流量换算

（1）、液体 （1atm，20℃清水为基准标定刻度）

    两式相比

         （7）  

根号这一项的数值，实际上是一个体积换算系数。

ρ水>ρ液，系数大于1

ρ水<ρ液，系数小于1

（2）、气体（1atm  20℃空气为基准标定刻度）

同理   

           （8）

3、改变转子密度

流量范围不变，改测大密度流体

设 ，即不论测何种液体，其流量刻度不变。

 ，

∴，       (9)

即，改成，就可以用水标定的刻度来测定的液体。也就是说，要改测大密度的液体，就换大密度的转子（反之亦然），但两个转子的形状和大小完全一样。

对于气体，同理

    （10）

§2-3 实际流体的流动

2-3.1 粘度

1. 牛顿型流体

（1）粘性

流体在运动状态下，有一种抗拒内在的向前运动的特性，称为粘性。流体不管在静止还是在流动状态下，都具有粘性，但只有在流体流动时才能显示出来。随流体状态的不同，粘性的差别非常悬殊。粘性是流动性的反面。 

实验证明：水在管内流过，由于粘性存在，管子任一截面上各点水的速度并不相等，管中心的速度最大，越靠近管壁速度越小。在贴近管壁的地方，有一层极薄的水粘附在管壁上，其速度=0。所以，在圆管内流动的流体，被剥离成无数个极薄的同心圆筒，一层套着一层，各层以不同的速度向前运动。靠中心的圆筒速度最大，稍靠外的圆筒的速度便小一些，前者对后者起带动作用，后者对前者便起拖曳的作用。筒与筒之间的相互作用就形成了流体阻力，这种阻力是在流体内部发生的。故称为内摩擦。这便是流体阻力的来源。

流体阻力大小的决定因素：

1、 流体自身的性质（粘度）

2、 流体的流动状况（流型）      主要

3、 管壁的粗糙度。               次要

  下面分别进行讨论。

（2）牛顿粘性定律

决定流体内摩擦大小的物理性质称为粘性。

衡量流体粘性大小的物理量称为粘度。粘性越大，流动性就越小。

A、粘度的物理意义

剪力：平行于作用面的力叫作剪力，用F表示。

剪应力：单位面积上的剪力叫剪应力。

在一平板上，相邻两层流体之间，若层间接触面积=A，层间距=

为使层间产生相对运动d，所需施加的剪力=F，

实验证明：F与A、d成正比，与d成反比。即

  或写成     （1）

此式叫牛顿粘性定律。

式中  —剪应力，Pa

—速度梯度，表示垂直于流动方向的速度变化率，1/s。

—比例系数，又叫粘滞系数，简称为粘度，Pa.S

服从牛顿粘性定律的流体称为牛顿型流体。

粘度的物理意义：

由（1）改写为，

促使流体流动产生单位速度梯度的剪应力。粘度总是以速度梯度相联系。所以，流体的粘度只有在它运动时才能显现出来。分析静止流体的规律时，就不用考虑粘度这个因素。

B、粘度的单位

（1）、cgs制  

1P=100Cp（厘泊）

（2）SI制

，∴，

C、温度、压强对粘度的影响。

液体：μ＝f（t）,与压强p无关,温度t↑,μ ↓。水（20℃）， μ ＝1.005cP；油的粘度可达几十、到几百Cp。

气体：气体的粘度随压强增加而增加得很少,在一般工程计算中可予以忽略,只有在极高或极低的压强下, 才需考虑压强对气体粘度的影响。 p<40atm时μ＝f（t）与p无关，温度t↑，μ↑

　　理想流体（实际不存在） ，流体无粘性μ＝0

D、粘度数据的来源

（1）查手册或共线图。

（2）用粘度计测定。

（3）用经验公式计算。

2-3.2 流体流动的型态

流体流动形态有两种截然不同的类型，一种是滞流（或层流）；另一种为湍流（或紊流）。两种流型在内部质点的运动方式，流动速度分布规律和流动阻力产生的原因都有所不同，但其根本的区别还在于质点运动方式的不同。

1、雷诺实验

Reynolds 英国学者，他在1883年做了如下实验。

          层流（滞流）

       过渡流

       湍流（紊流）

采用不同的管径d、流速、粘度、密度，分别作实验，最后归纳为雷诺准数：

不论采用什么单位制，Re均无因次，凡是由几个有内在联系的物理量按无因次这个条件组合起来的数群，称为准数。

在化工生产中，不但有圆管，还有非圆形的，对于非圆形管内的流体流动，找一个与直径相当的量，Re才能算出，为此引入水力半径这个概念。水力半径的定义式为，

对于圆管， 

∴，圆管直径d = 4水力半径 = 4Rh

非圆形管就采用4倍的水力半径代替直径。即当量直径 de=4水力半径。

对于长方形管，（a，b）

环形，外管内径d1，内管外径d2，（P92有套管换热器图）。

那么  

注意：不能用de计算非圆形截面导管或设备的截面积，流速和流量。

2、流动类型

雷诺准数这个数群，既反映了所包含的各个物理量的内在联系，又说明了流动流型的本质。所以，流体的流动类型就可以由Re来判断。实验证明：

  Re <2000           为层流

  Re >4000            湍流

  2000<Re<4000       过渡流

3、层流与湍流的区别

4、边界层的概念

A、平板上的流动边界层

流体流动受固体壁面影响（能感受到固体壁面存在）的区域。

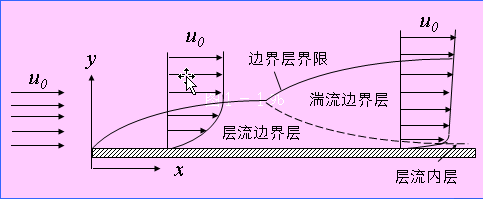
边界层：流体的流速低于未受壁面影响的流速的99%的区域。

主流区：在边界层以外，速度梯度接近为零的区域。

B、圆管入口处的流动边界层发展

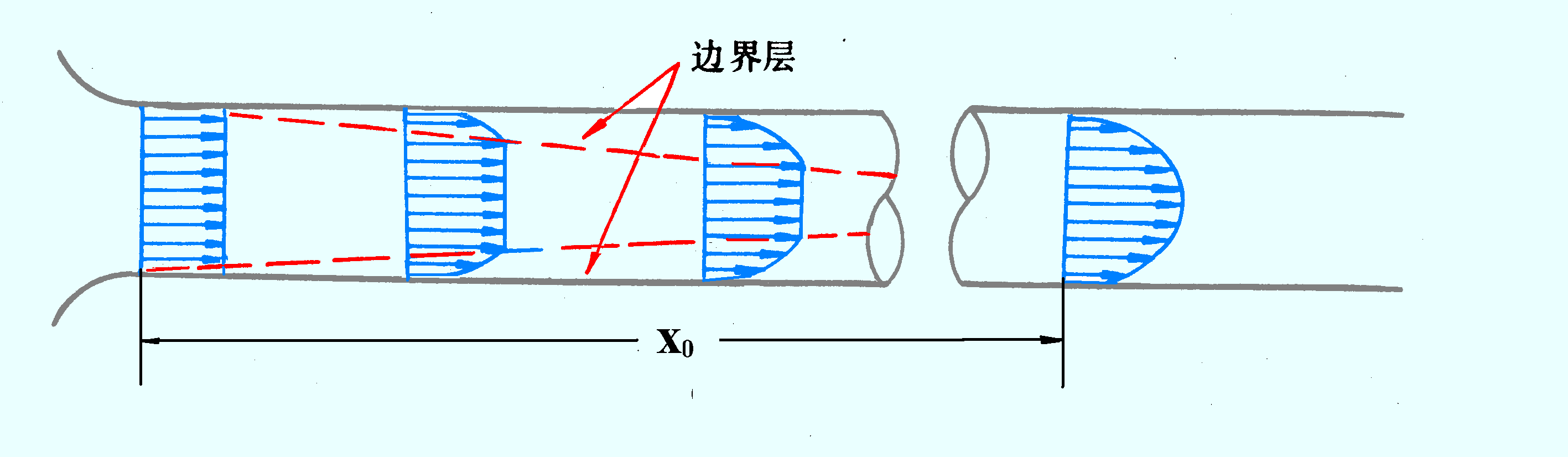
内摩擦：一流体层由于粘性的作用使与其相邻的流体层减速。

边界层：受内摩擦影响而产生速度梯度。

稳定段长度：从管口到形成边界层所经历的管长，其长度与管的形状、管壁粗糙度及雷诺准数等因素有关。

边界层发展：边界层厚度d 随流动距离增加而增加。

流动充分发展：边界层不再改变，管内流动状态也维持不变，充分发展的管内流型属层流还是湍流取决于汇合点处边界层内的流动属层流还是湍流。 

C、流体在圆管内的速度分布

滞流时的速度分布  理论分析和实验都已证明，滞流时的速度沿管径按抛物线的规律分布，如图所示。截面上各点速度的平均值等于管中心处最大速度umax的0.5倍。

湍流时的速度分布  湍流时流体质点的运动情况比较复杂，目前还不能完全采用理论方法得出湍流时的速度分布规律。经实验测定，湍流时圆管内的速度分布曲线如图所示。速度分布比较均匀，速度分布曲线不再是严格的抛物线。管内流体的平均流速为管中央最大流速的0.8倍左右。

D、流体流过曲面或障碍时的边界层分离

当流体流过曲面或障碍时，还会发生边界层分离现象。

§2-4 流体在圆管内流动时的阻力计算

2－4.1 滞留时的摩擦阻力

流体在管内以一定的速度流动时，有两个方向相反的力互相作用着。

1、推动力（促使流体流动），和流动方向一致。

2、摩擦阻力（由内摩擦引起），与流动方向相反。

当推动力与阻力达于平衡，流速才能维持不变，即达到稳定流动。

在圆管内取一圆柱形的流体单元，其半径为r，在一个半径为r+dr的流体圆筒内滑动。这个流体单元的推动力与阻力的关系可表示为：

             （3）

即       （6）

根据牛顿粘性定律，圆筒内的剪应力为  （7）

：距管中心线r处的流体流速。

由于r越大，越靠近管壁。即与r的大小变化相反，故加“－”号。

把（7）代入（6）得

，

      分离变量积分：

根据边界条件，确定C。

当r = R时，=0  （靠管壁） 

∴，

           （8）

流体通过环隙的体积流量

从管中心到管壁积分，得整个管截面的体积流量。

       将（8）代入

         联立

，   （9）

上式为哈根—泊稷叶公式，此式为计算层流时由摩擦阻力所引起的压强降公式。

将Re代入上式得：

或    

2－4.2   湍留时的摩擦阻力

 根据多方面得实验并进行适当数据处理后，得到如下公式：

                     或

--------称为摩擦阻力系数，是Re数的函数

上式为计算直管阻力的通式，叫范宁公式。此方程对于滞流与湍流均适用。

壁粗糙度对的影响

化工管路按其材质和加工情况可分为：

光滑管  如，铜、 铅、玻璃、塑料

粗糙管  如， 钢、 铸铁管

管壁粗糙度可用绝对粗糙度和相对粗糙度表示。

绝对粗糙度：e，表示管壁凹凸部分的平均高度。

相对粗糙度：是绝对粗糙度与管径之比。

对于e相同的管子，e对的影响与管径有关。对d小的影响大。因此，工程上不是只看e的大小，而是看的大小。

层流时：光滑管与粗糙管的—Re关系标绘在图上为同一根直线（P48图）。说明管子的粗糙度对无影响。

湍流时：若滞流内层厚度，如图a，此时e（或e/d）对无影响。

     若，变薄，使，e（或e/d）对有影响。如图b。

湍流时的

由于湍流比滞流情况复杂得多，因此，湍流时的就不能用理论分析法来求得解答。目前主要用因次分析法来处理湍流时的。

通过因次分析，认为，其具体的函数关系需由实验确定。将实验数据进行综合整理，以Re，e/d为参数，对作图。其结果如P48图所示。 

用光滑管于Re=3103~1105范围内作实验，所得数据经处理得到：

上式称为柏拉修斯公式。

2－4.3 局部阻力的计算

当量长度法  流体通过某一管件或阀门时，因局部阻力造成的压头损失，相当于流体通过与其具有相同管径的若干m长度的直管的压头损失，这个直管长度称为当量长度，用Le表示。那么局部阻力为：

§2-5  离心泵

一、工作原理

离心泵主要部件是叶轮和泵壳。

叶轮是对液体作功的部件。

泵壳是离心泵的外壳。在泵壳内有一个截面逐渐扩大的蜗牛壳形通道，所以又称为蜗壳。

离心泵开启前，先要用被输送的液体将泵体灌满，在压出阀门关闭的情况下启动电机，然后开启压出阀。叶轮高速旋转，产生离心力，液体被甩向叶轮外缘，液体获得了动能，液体在渐扩通道内流速，一部分动能转化为静压能。泵出口液体。液体被压出，由于离心力的作用，叶轮中心区形成负压，因此液体被吸入泵体。（液体被吸入压出）。

离心力的大小，与叶轮转速

                叶轮大小       有关

                液体的密度

液体的密度越大，产生的离心力也越大，所以开泵前要灌满液体，而把空气挤出，否则离心泵则不能输送液体。因为气体密度小，产生的离心力小，叶轮中心产生的负压小，不能将液体吸入和压出，这种现象称为“气缚”。

二、主要性能参数

1、扬程

扬程又称为泵的压头，是泵对单位质量的流体提供的能量。用H表示。

2、流量

单位时间排出的液体体积  [ m3/h]，

与泵结构

    叶轮尺寸     有关，通常由实验测得。

    转速

3、功率

       轴功率（实际功率）：①泵轴从电机得到的实际功率称轴功率。

功率                       ②电机直接传动，传给泵轴的功率，以Pa表示，[W]      

 理论功率：Pe表示。

轴功率

泵的效率 <1

三、特性曲线

离心泵的特性曲线是分析和选用泵的重要依据。它反映了泵的、H、 和轴功率Pa之间的相互关系，一般离心泵产品样本上提供的特性曲线为

H——

Pa——      三条曲线

——

以上三条曲线是在常温、常压下，在一定转速下，用清水作实验测得的。若输送的液体其物性与水差异较大，则需对曲线进行换算。

1、H—曲线 （扬程曲线）

扬程H随流量增大而减小。

2、—曲线（功率曲线）

轴功率随流量增加而增加。=0时，最小，所以泵在启动时关闭出口阀，使泵在最低功率下启动，保证电机不超载。

3、—曲线（效率曲线）

   =0时，最低

增加，也增加，达最大值后，再↑，↓，峰值为最高效率点。

    泵的最高效率点即为泵的设计点，标注在铭牌上的数值，就是与此点对应的各性能参数。

泵在铭牌上标出的流量及扬程下工作最为经济，但根据输送条件的不同，往往不能在最高效率下操作，所以规定一个工作范围，通常将最高效率的92%这个范围称为泵的最高效率区，选用离心泵时，应尽可能使泵在此范围工作。

四、安装高度

以1—1’，2—2’为截面，0—0’为基准面，则柏式

H1=0，H2=Hg， 

∴，

  令   ——允许吸上真空高度。

安装高度：       （1）

上式即为离心泵安装高度的计算式。

                输送液体的密度

                泵吸入口处压强P2

安装高度与      当地大气压 P1

                泵的转速  n

                流量等，多种因素有关

泵入口处的压强P2越小，Hs越大，则泵的安装高度Hg越大，但P2有一极限值，即P2>输送液体的饱和蒸气压。否则，吸入液体就会在泵中心处气化，体积突然膨胀。当含有大量气泡的液体由低压区进入高压区时，气泡受压而迅速凝结，因而形成局部真空，周围的液体便以极大的速度冲向原来气泡所在的空间，在冲击点上产生几百大气压的局部压强，使叶轮遭到破坏，这种现象称为“气蚀”。气蚀发生后，泵体震动，产生明显噪音，泵的流量、扬程、效率显著降低。必须避免。

：吸入管的动压头，  ↓则Hg大。

所以，通常让吸入管径大于排出管径，以减小吸入管的动压头，从而增大安装高度Hg。

泵的允许吸上真空高度Hs由制造厂实验测定。其测定条件是在1大气压下用20℃清水。如果输送时的条件与上述条件不同，则对Hs进行换算，其换算公式如下：

Hs’=Hs－10+Ha－Ht

式中  Hs’——输送条件下的允许吸上真空高度，m

Hs——说明书上查得的数值， m

      Ha——泵工作地点大气压 ，m水柱

      Ht——输送温度下水的饱和蒸气压，m水柱