第二节 地图投影分类
1.按变形性质分类
1.1 等角投影
投影面上任意两方向线间的夹角与椭球面上相应两方向线的夹角相等，即ω＝0。等角投影地图上无角度变形，变形椭圆为圆，常用于编制航海图、交通图、洋流图等。
1.2 等积投影
投影面上任意一块图形的面积与椭球面上相应图形的面积相等，即VP＝0。等积投影地图上无面积变形，但图形轮廓形状变形很大，常用于编制对面积量算要求较高的自然地图和社会经济地图。
1.3 任意投影
任意投影既存在角度变形，也存在面积变形，但是角度变形小于等积投影，面积变形小于等角投影。这类投影多用于编制教学地图、参考地图、宣传地图等。
★ 任意投影中有一类投影沿特定方向没有长度变形，即 a＝1或 b＝1，这类投影称为等距投影。
2.按投影的构成方法分类
2.1 几何投影
（1）方位投影
以平面为投影面，使平面与椭球体相切或相割，将球面经纬线网投影到平面上（图3-7）。

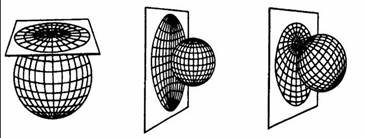
                  图3-7 方位投影原理
方位投影的切点或割线没有变形，离开没有变形的点或线越远变形越大，等变形线呈同心圆分布。
（2）圆柱投影
以圆柱面为投影面，使圆柱面与椭球体相切或相割，将球面经纬线网投影到圆柱面上，然后展开成平面（图3-8）。

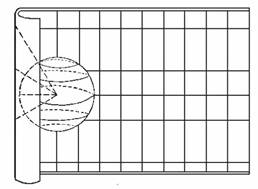
             图3-8 圆柱投影原理
圆柱投影的切线或割线没有变形，离开没有变形的线越远变形越大。正轴圆柱投影的等变形线是一组平行直线。
（3）圆锥投影
以圆锥面为投影面，使圆锥面与椭球体相切或相割，将球面经纬线网投影到圆锥面上，然后展开成平面（图3-9）。

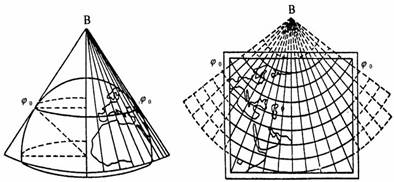
                     图3-9 圆锥投影原理
圆锥投影的切线或割线没有变形，离开没有变形的线越远变形越大。正轴圆锥投影的等变形线是一组与纬线平行的同心圆弧。
★ 根据投影面与椭球面的位置关系，方位投影、圆柱投影、圆锥投影都有正轴、横轴和斜轴三种类型（图3-10）。

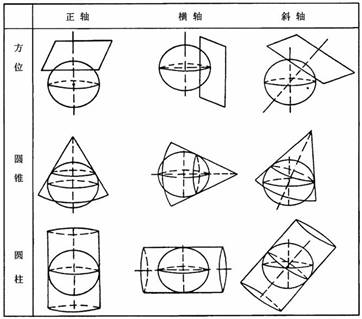
             图3-10 投影面与椭球面的位置关系
2.2 条件投影
也称解析投影。在特定要求的基础上选择投影条件，利用数学解析方法建立球面与平面之间对应点的函数关系，然后将球面经纬线网转绘到平面上。
（1）伪方位投影
根据方位投影修改而来的条件投影。纬线仍为同心圆，中央经线为直线，其余经线为对称于中央经线的曲线（图3-11）。

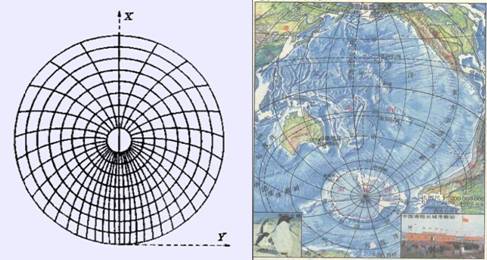
                            图3-11 伪方位投影及其应用
（2）伪圆柱投影
根据圆柱投影修改而来的条件投影。纬线仍为平行直线，中央经线为直线，其余经线为凹向且对称于中央经线的曲线（图3-12）。

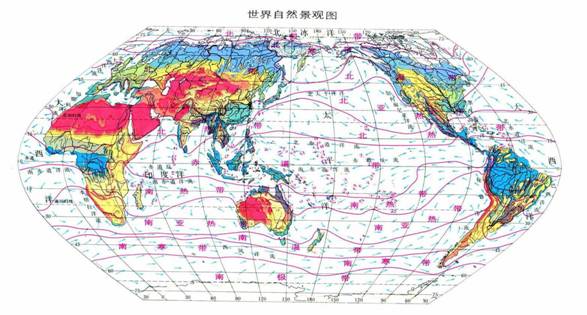
                                      图3-12 伪圆柱投影的应用
（3）伪圆锥投影
根据圆锥投影修改而来的条件投影。纬线仍为同心圆弧，圆心在中央经线上，中央经线为直线，其余经线为凹向且对称于中央经线的曲线（图3-13）。

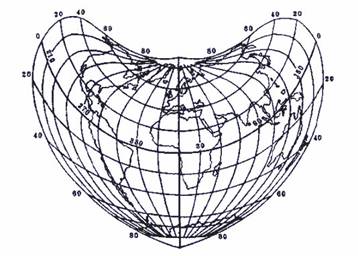
                    图3-13 伪圆锥投影
（4）多圆锥投影
假设用许多圆锥面按预定间隔套在椭球体上并与椭球面相切，然后将椭球面上的经纬网投影到各圆锥面上，再沿某一经线将各圆锥面切开展平得到的条件投影（图3-14）。

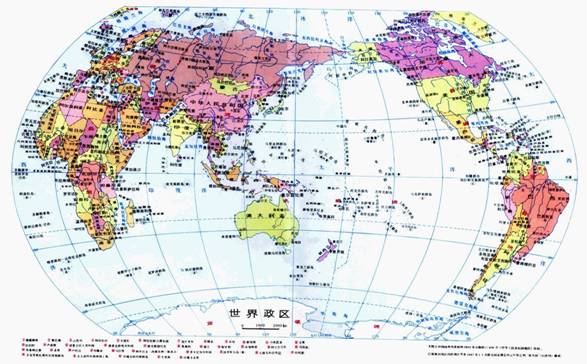
                                     图3-14 多圆锥投影的应用