第一节 地图投影概述
1.地图投影的概念
1.1 地图投影的定义
按照一定的数学法则将球面上的经纬网转移到平面上的方法（图3-1）。地图投影的本质是建立球面点与平面点之间的函数关系：
x ＝ f1(λ，φ)
y ＝ f2(λ，φ)

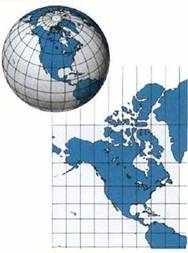
      图3-1 球面到平面的转换
1.2 地图投影的基本方法
（1）几何透视法
利用透视关系将球面经纬网投影到投影面上的方法。投影面为平面，或可展开成平面的曲面，如圆柱面、圆锥面。

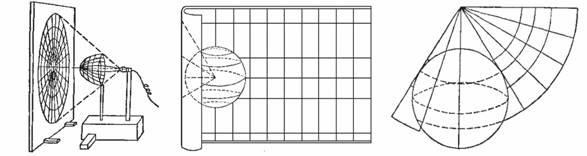
                                      图3-2 几何透视法
（2）数学解析法
通过数学方法建立球面点与投影面点之间函数关系，以确定经纬线交点的平面坐标位置的方法。
★ 以球面方位投影为例，通过数学解析法可得该投影的极坐标方程（图3-3）：
ρ＝2R·tg((90°-φ)/2)
δ＝λ

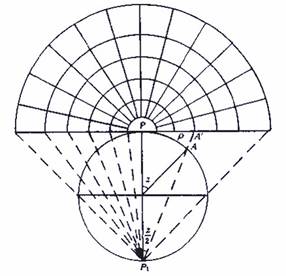
      图3-3 数学解析法求取球面方位投影方程
2.地图投影变形
2.1 地图投影变形的概念
指球面转换成平面后地图上所产生的长度、角度和面积误差。
★ 任何地图投影都存在投影变形。
★ 投影变形可用变形分布表（表3-1）、等变形线（图3-4）、变形椭圆描述（图3-5）。
                                                    

                     表3-1 高斯-克吕格投影6°带内长度变形表                     

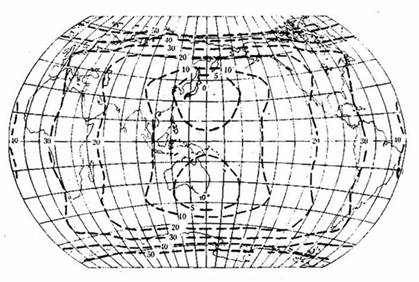
               图3-4 等差分纬线多圆锥投影的角度等变形线

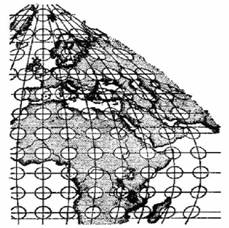
   图3-5 变形椭圆表示投影变形的分布
2.2 地图投影变形的性质和大小
（1）长度比与长度变形
投影面上一微小线段ds’与椭球面上相应微小线段ds的比值称为长度比。
μ＝ ds’/ds
式中：μ＞1，表明投影后长度拉长；μ＜1，表明投影后长度缩短；μ＝1，表明投影后长度没有变化。
长度变形是长度比与1的差值：
Vμ＝ μ－1
通常用a、b表示最大和最小长度比，用m、n表示纬线和经线长度比，且存在下列关系：
m2＋n2＝ a2＋b2
mnsinθ ＝ab
或
（a＋b）2 ＝ m2＋n2 ＋2 mnsinθ
（a－b）2 ＝ m2＋n2 －2 mnsinθ
当投影后经纬线呈直角相交，则经纬线长度比为最大、最小长度比。
（2）面积比与面积变形
投影面上一微小面积dF ’与椭球面上相应微小面积dF的比值称为面积比。
P＝dF ’/dF ＝πarbr/πr2＝ab＝mnsinθ
式中： P ＞1，表明投影后面积变大；P ＜1，表明投影后面积缩小；P ＝1，表明投影后面积没有变化。
面积变形是指面积比与1的差值：
VP＝ P－1
（3）角度变形与最大角度变形
投影面上任意两方向线的夹角与椭球面上相应两方向线的夹角之差称为角度变形。
最大角度变形的计算：
sinω/2 ＝（a－b）/（a＋b）
  ＝((m2＋n2 －2mnsinθ)/(m2＋n2＋2 mnsinθ))1/2
角度变形引起图形形状的变化，当最大角度变形ω＝0时，变形椭圆表现为圆。
2.3 变形椭圆
1881年，法国数学家底索(Tissot)首先发表了变形椭圆理论，证明球面上的微圆投影到平面上必然为一微椭圆，即变形椭圆，也称底索曲线(Tissot’s indicatrix)。
设沿纬线、经线方向的长度比为m、n，则由图3-6得：

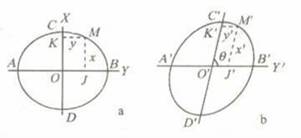
             图3-6 变形椭圆原理
x＝x’/m；  y＝y’/n
又微圆方程为：
x2＋y2＝1
将前式代入圆方程得：
x’2/m2＋y’2/n2＝1