第九章：化学动力学

1．了解化学反应速度的表示方法及计算。

    2．掌握速度方程式和反应级数的概念。

    3．了解活化能的概念及浓度、温度、催化剂对化学反陵速度的影响。  

4．掌握有关阿累尼乌斯公式的计算。

（重点复习）

化学动力学就是解决化学反应进行的速度及历程问题。化学动力学的基本任务是研究反应进行的条件——浓度、温度、压力、催化剂等对反应速度的影响，和揭示化学反应的历程，其最终目的是为了管理和控制化学生产过程。

 (一)化学反应速度的表示法

    化学反应速度以单位时间内作用物的浓度减少或生成物的浓度增加来表示。

    有两种表示方法（1）平均速度 （2）瞬时速度

    1．平均速度：某一区间的平均速率。

例如对于反应  aA+bB＝cC+dD

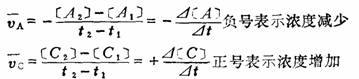
2．瞬时速度：

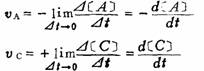
注意研究某一化学反应速度与浓度的关系，应该固定选用一种作用物或生成物来表示。它们之间的关系为

    (二)反应速度和浓度的关系及速度方程式

    1．对于基元反应，化学反应速度与反应物浓度以反应分子数为乘幂的乘积成正比。这个定律叫质量作用定律。例如

    aA+bB＝cC+dD              v = k[A]^a[B]^b

上式称为速度方程式，k 称为速度常数，k 与反应物的浓度无关与温度有关。

2．许多化学反应不是基元反应，而是分步完成的，反应速度与浓度关系不能由上式表示，化学反应速度是由最慢一步反应的速度决定。例如

2NO_(g) +F_{2 (g)} =2NOF_(g)             反应分两步进行

    (I)  NO_(g) + F_2(g)＝NOF_2(g)    (慢)

    (II)NOF_{2 (g)} + NO_(g)＝2NOF_(g)  (快)

第一步基无反应是慢反应，它决定总反应的反应速度，称为定速反应。所以反应速度方程式为  

    v = k[NO][F₂]

3．对于一个化学反应，如果不知道反应历程，不能任意写出速度方程式，必须由实验数据决定。

(三)反应级数及反应级数的判定

1．反应级数由反应速度方程式v = k[A]^x[B]^y决定，此反应对于A为x级反应，对于B为y级反应，反应总级数等于x+y。

2．尝试法求反应级数。

    通过一些量对时间作图，根据成直线关系的结果，可以求出反应级数，这是探求反应机理中常用的方法，称为尝试法求反应级数。

    3．根据速度方程式中，反应速度常数k的单位，可以判别反应级数：

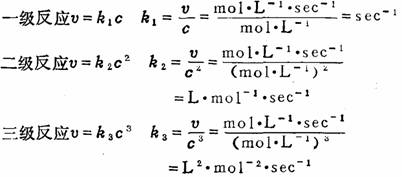
    4．由反应级数探求反应机理  当反应级数与反应计量方程式系数不符合时，肯定为分步反应，由此探求反应机理。

探求反应机理应注意几点：

    (1)反应机理必须符合反应速度方程式。

    (2)分步反应总和一般等于总反应方程式。

    (3)中间产物能否存在必须根据实验来验证。

例如，一氧化碳和二氧化氮之间的反应

    NO₂ + CO＝CO₂ + NO

    在温度高于500K时，v＝k[NO₂][CO]反应级数与反应计量方程式系数相符合，此反应为一步完成基元反应。

    在较低温度时，v＝k[NO₂]²从速度方程式可知，反应速度与NO₂浓度平方成正比而与CO浓度无关。反应级数与反应计量方程式系数不符合，有人提出如下反应机理作解释：

    (I)NO2 + NO2＝NO3 + NO        (慢)

    (II)NO3 + CO＝NO2 + CO2       (快)

由于第一步是侵反应，是定违反应，所以反应速度方程

    v＝k[NO₂]²

    两步反应总和等于总反应方程式。至于这反应机理能否成立，决定于用分子光谱能否发现中间产物NO₃。

当反应级数与反应速度方程式相符合时，也不一定是基元反应，例如

    H_2(g) + I_2(g)＝2HI_(g)

根据实验结果，其速度方程式为

   v＝k[H₂][I₂]

半个多世纪一直误认为它是一个一步完成的简单反应。但是近年来，不论从实验或理论上都表明，它不是一步完成的基元反应，其反应机理可能是：

    (I)    I2＝2I    (快)

    (II)    2I + H2＝2HI  (慢)

反应速度方程式由慢反应决定：

    V＝k₂[H₂][I]²

基元反应(II)是在基元反应(I)已达平衡的基础上进行的。根据反应(I)有：

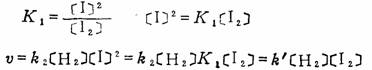
    上述结果表明，基元反应(II)虽是一个三分子反应，但当用[H₂]和[I₂]表示时，  完全与由实验得出的速度方程式相吻合。这就是长期将该反应看作是一步完成双分子反应的原因。最近也有人对这个反应机理提出不同的看法。总之，反应机理是一个十分复杂的问题，在已知的化学反应中，巳完全弄清反应机理的为数不多，这主要是由于化学反应历程的复杂性和实验技术的限制所造成的。

    (四)活化能及温度、浓度、催比剂对反应速度的影响

    在理论发展过程中，随着不同的历史条件，先后形成了两个速度理论：碰撞理论与过渡状态理论。

    要点：化学反应只有分子间有效碰撞才能产生，即分子动能大于某临累值E_c，分子碰撞才能发生反应。

    1．活化能：  E_a＝E_c—E_平均

    即一定温度下，活化分子具有的最低能量与分子平均能量之差称为活化能。

    2．活化分子：能量大于等于活化能的分子称为活化分子。

    (1)不同反应具有不同活化能，反应活化能越低，活化分子的百分数越大，反应速度越快。所以化学反应速度常数k决定于反应物本质。

    (2)浓度越大，活化分子数目越多，反应速度越快。

    (3)温度升高，活化分子百分数增大，反应速度增快。范待荷夫规则认为：温度每升高10℃，反应速度增加为原来的2~3倍。此规则仅适用于一定活化能范围及一定温度范围。活化能越大，温度升高10℃，反应速度增加的倍数越大。

    (4)催化剂能大大提高反应速度达几千倍或几万倍，其本质是降低反应的活化能。在均相催化剂中主要是形成中间产物，降低反应的活化能。非均相催化剂主要提供活性中心，通过吸附作用降低反应的活化能。

    3．活化能的实质：高能分子相碰撞，克服反应中的势能。按照过渡状态理论，在反应分子之间的一次有效碰撞过程中，两种分子可以生成一种不稳定的过渡状态物质，称为活化配合物，例如反应。

    A + B-C＝A…B…C＝A-B + C

在发生化学反应时，反应物A与B-C作用生成A-B与C的过程中间，要经过一个吸收能量Ea达到活化状态A…B…C的过程(A…B…C称为活化配合物)。A…B…C很不稳定，分解生成AB和C，只有总能量比反应物分子平均能量至少高出Ea的分子，才能越过能峰变成生成物分子。Ea为正反应活化能。同样，对于逆反应来说，生成物必须吸收Ea'能量，达到活化状态A…B…C，而后进行反应生成A-B和C。Ea'为逆反应活化能。

(五)阿仑尼乌斯公式及有关计露

1889年，阿仑尼乌斯提出反应速度与温度关系的经验式：

积分(1)式，可得

    式中Ea——活化能；

    R——气体常数8．315J.mol^-1．K^-1；

    A——积分常数。

以lnk为纵坐标对1/ T作图，可得一直线，  直线的斜率为-Ea/R，由此可以求出反应的活化能，除了作图法计算活化能外，更重要的是使用下面的公式直接进行计算:

    (3)式可由(2)式推得。该公式的应用如下：

(a)使用公式(2)和(3)，可以从两个不同温度(T₁，T₂)下的反应速度常数(k₁，k₂)求活化能。

(b)巳知活化能Ea及某一温度T₁的k₁值，就可代入(3)式求另一温度T₂的k₂值。

(c)利用公式可求活化能大小对反应速度常数的影响。