第十一章:电化学基础
1.牢固掌握氧化还原的基本概念,并能熟练掌握氧化还原反应方程式的配平。
2.熟练运用标准电极电势估计和判断氧化剂和还原剂的强弱、氧化还原反应进行的方向及反应进行的程度。
3.了解电解、电解定律及其应用。
重点复习
(一)基本概念
氧化还原反应是指元素有氧化数变化的反应。例如下列反应:

在反应中氧化数降低的物质Cl2 为氧化剂;氧化数升高的物质KI为还原剂。还原剂在反应中发生氧化反应,自身被氧化,氧化剂在反应中发生还原反应,自身被还原。所以氧化和还原必然同时发生。
(二)氧化还原反应方程式的配平
1.氧化数法
以氯酸与磷反应为例,说明用氧化数法配平氧化还原反应式的步骤:
(1)写出基本反应式
HClO3 + P4 → HCl + H3PO4
(2)找出氧化剂中原子氧化数降低的数值和还原剂中原子氧化数升高的数值。
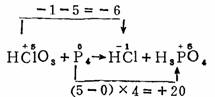
(3)调整系数,使氧化数升高的总数等于氧化数降低的总数。
![]()
(4)在氧化剂和还原剂的化学式前,各乘以相应的系数。并使方程式两边相应的原子数相等。
10HClO3 + 3P4 →10 HCl + 12H3PO4
(5)配平反应前后氧化数未发生变化的原子数。首先检查反应方程式两边的氢原子数目,找出参加反应的水分子数。最后核对氧原子数。
由于右边多36个氢原子和18个氧原子,左边应加18个水分子,得到配平了的氧化还原方程式。
10HClO3 + 3P4 + 18H2O →10 HCl + 12H3PO4
2.离子—电子法
离子—电子法和氧化数法配平的原则相似。它的原则是在氧化还原反应中,得失电子数相等。以高锰酸钾与盐酸作用为例来说明离子-电子法的配平步骤。
(1)先将反应物的氧化还原产物,以离子形式写出。
MnO4- + Cl- → Mn2+ + Cl2
(2)将这个反应式分为两个半反应,一个被氧化;一个被还原。
C1- → C12 (氧化)
MnO4- → Mn2+ (还原)
(3)分别配平两个半反应式的原子数,然后配平电荷数
2C1- → C12 + 2e
MnO4- +8H+ + 5e → Mn2+ + 4H2O
(4)合并半反应方程式。并使还原反应得电子致等于氧化反应中失电子数。
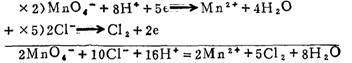
(三)原电池和电极电势
1. 原电池
原电池是将氧化还原反应的化学能直接转变为电能的装置。
原电池由2个半电池组成,负极失电子被氧化,正极得电子被还原。例如Cu—Zn原电池中的反应如下:
锌电极:氧化反应 Zn → Zn2+ + 2e
铜电极:还原反应 Cu2+ +2 e → Cu
电池反应:氧化还原反应 Zn + Cu2+ = Zn2+ + Cu
以铜锌原电池为例,将各种术语及表示方法列表如下:
|
电极名称 |
负极 |
正极 |
|
电极反应 |
Zn=Zn2++2e(氧化反应) Zn(还原剂) |
Cu2++2e=Cu(还原反应) Cu2+(氧化剂) |
|
电池反应 |
Zn +Cu2+= Zn2++ Cu(氧化还原反应) |
|
|
电极电势 |
Ezn2+/Zn |
ECu2+/Cu |
|
电池电动势 电池符号 |
ε=E(+)--E(-);ε= ECu2+/Cu-- Ezn2+/Zn (一)Zn|Zn2+(1M)‖Cu2+(1M)|Cu(+) |
|
2.电极电势
电极电势是如何产生的?当把金属置于其盐溶液中时,便存在两种趋势:
![]()
(I)为金属正离子的溶解趋势;
(II)为溶液中金属正离子沉积的趋势。
当这两种趋势达到动态平衡时,无论第(I)种趋势大于第(II)种趋势或是小于第(II)种趋势,金属与它的盐溶液间都会形成双电层,这种双电层产生电极电势。
3.标准氢电极和标准电极电势
如何测定电极电势的数值,电极电势的绝对值迄今仍无法测量。只能选定某种电极作为标准,其他电极与之比较,求得电极电势的相对值,通常选定的是标准氢电极。
标准氢电极是这样构成的:将镀有铂黑的铂片置于氢离子浓度为1M的硫酸溶液中,然后在298K时不断地通入压力为lat m的纯氢气,使铂黑吸附氢气达到饱和,形成一个氢电极,在这个电极的周围发生了如下的平衡: H2 = 2H+ + 2e
这时产生在标准氢电极和硫酸溶液之间的电势,叫做氢的标准电极电势,将它作为电极电势的相对标准,并令其为零。
用标准氢电极与其他各种标准状态下的电极组成原电池,测得这些电池的电动势,从而计算各种电极的标准电极电势。
(四)电油的电动势与反应自由能变的关系
εo与⊿Go之间的关系可从热力学的论证中得到:
-⊿Go=nFεo
其中⊿Go是用千焦表示的标准自由能变化,n是反应中电子的转移数,F是1mol电子所带的电量,其数值为96500c/mol,εo是标准电池电动势。
根据上式,可以从电他的电动势计算氢化还原反应的自由能变化或从热力学数据计算原电池的电动势。
(五)原电池的电动势与平衡常数的关系
在化学热力学一章中指出,标准自由能变化⊿Go与平衡常数有如下的关系:
⊿Go=-2.303RTlgK
所以得到 nFεo=2.303RTlgK
在298K
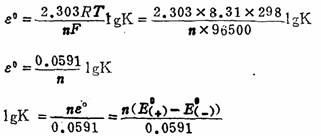
根据上式,可从电池的电动势计算氧化还原反应的平衡常数,确定反应进行的程度 。
(六)浓度对电极电势的影响—奈斯特方程
对于一般的氧化-还原反应
aA + bB = cC + dD
当温度为25℃时,奈斯特方程为
![]()
电极反应的通式为: 氧化型 + ne =还原型
其奈斯特方程可写为:
![]()
式中E是指定浓度下的电极电势;Eo是标准电汲电势,n是电极反应中得到或失去的电子数;[氧化型]或[还原型]表示氧化型物质或还原型物质体积摩尔浓度(严格地说应为活度)。
应用奈斯特方程时应注意以下几点:
(1)方程式中的[氧化型]和[还原型]并非专指氧化数有变化的物质,而是包括了参加电极反应的其他物质。
(2)电极反应中纯固体、纯液体的浓度为常数,作1 处理。气体用分压表示。
(3)电极反应式中的系数为浓度或分压的指数。
(七)电极电势的应用
1.判断氧化剂和还原剂的相对强弱
电极电势代数值的大小反映了电对中氧化型物质得电子能力和还原型物质失电子能力的大小。
我们可看到在标准电极电势表中存在着下列关系:

可见,表中最强的还原剂为Li,最强的氧化剂是F2;相应的Li+是最弱的氧化剂,F-则是最弱的还原剂。
2. 判断氧化还原反应进行的方向
反应自发进行的条件为 ⊿G<0
3.估计氧化还原反应进行的程度
根据εo和K之间的关系以及反应物的已知起始浓度,可以确定反应发生的程度。
4.已知εo求平衡常数
通过上述例题得知,可以利用测定原电池电动势的方法来确定氧化还原反应的平衡常数,对其它类型反应的平衡常数,如弱酸的电离常数、难溶电解质的溶度积常数等也可用测定原电池电动势的方法来确定。
(八)元素标准电极电势图及其应用
当某元素可能有三种或三种以上氧化态的物质时,这些物质可以组成多种不同电对,各电对的标准电极电势的相互关系能够以图的形式表示出来,这种图叫做元素电势图。
从元素电势团不仅可以全面地看出一种元素各氧化态之间的电极电势高低和相互关系,而且可以判断哪些氧化态在酸性或在碱性溶液中能否稳定存在。以下介绍几方面的应用。
1.判断歧化反应是否能够进行
2.求算某电对的未知的标准电极电势
根据热力学已推导出的公式(若有i个相邻电对):

式中n1、n2、n3、.....、ni分别表示各相应电对中所转移的电子数。